Question

【题目】已知函数u（x）＝xlnx，v（x）x﹣1，m∈R．

（1）令m＝2，求函数h（x）的单调区间；

（2）令f（x）＝u（x）﹣v（x），若函数f（x）恰有两个极值点x1，x2，且满足1e（e为自然对数的底数）求x1x2的最大值．

Answer 1

【答案】（1）单调递增区间是（0，e），单调递减区间是（e，+∞）（2）

【解析】

（1）化简函数h（x），求导，根据导数和函数的单调性的关系即可求出

（2）函数f（x）恰有两个极值点x1，x2，则f′（x）＝lnx﹣mx＝0有两个正根，由此得到m（x2﹣x1）＝lnx2﹣lnx1，m（x2+x1）＝lnx2+lnx1，消参数m化简整理可得ln（x1x2）＝ln，设t，构造函数g（t）＝（）lnt，利用导数判断函数的单调性，求出函数的最大值即可求出x1x2的最大值．

（1）令m＝2，函数h（x），∴h′（x），

令h′（x）＝0，解得x＝e，

∴当x∈（0，e）时，h′（x）＞0，当x∈（e，+∞）时，h′（x）＜0，

∴函数h（x）单调递增区间是（0，e），单调递减区间是（e，+∞）

（2）f（x）＝u（x）﹣v（x）＝xlnxx+1，

∴f′（x）＝1+lnx﹣mx﹣1＝lnx﹣mx，

∵函数f（x）恰有两个极值点x1，x2，

∴f′（x）＝lnx﹣mx＝0有两个不等正根，

∴lnx1﹣mx1＝0，lnx2﹣mx2＝0，

两式相减可得lnx2﹣lnx1＝m（x2﹣x1），

两式相加可得m（x2+x1）＝lnx2+lnx1，

∴

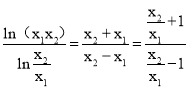
∴ln（x1x2）＝ln，

设t，∵1e，∴1＜t≤e，

设g（t）＝（）lnt，∴g′（t），

令φ（t）＝t2﹣1﹣2tlnt，∴φ′（t）＝2t﹣2（1+lnt）＝2（t﹣1﹣lnt），

再令p（t）＝t﹣1﹣lnt，∴p′（t）＝10恒成立，

∴p（t）在（1，e]单调递增，∴φ′（t）＝p（t）＞p（1）＝1﹣1﹣ln1＝0，

∴φ（t）在（1，e]单调递增，∴g′（t）＝φ（t）＞φ（1）＝1﹣1﹣2ln1＝0，

∴g（t）在（1，e]单调递增，∴g（t）max＝g（e），

∴ln（x1x2），∴x1x2

故x1x2的最大值为．