Question

【题目】已知倾斜角为的直线经过抛物线：的焦点，与抛物线相交于、两点，且.

（Ⅰ）求抛物线的方程；

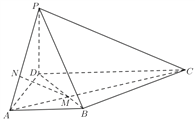
（Ⅱ）过点的两条直线、分别交抛物线于点、和、，线段和的中点分别为、.如果直线与的斜率之积等于1，求证：直线经过一定点.

Answer 1

【答案】(Ⅰ)；(Ⅱ)证明见解析.

【解析】分析：（Ⅰ）由题意可设直线的方程为，与抛物线方程联立可得，由弦长公式可得，则,抛物线的方程为.

（Ⅱ）设直线的斜率为，则直线的斜率为.则直线的方程为，与抛物线方程联立可得，据此可得，同理可得：，直线的方程为，即，直线经过定点.

详解：（Ⅰ）由题意可设直线的方程为，令，.

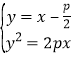联立得，∴，

根据抛物线的定义得，又，又，∴，∴.

则此抛物线的方程为.

（Ⅱ）设直线的斜率为，则直线的斜率为.

于是直线的方程为，即，

联立得，∴，

则，∴，

同理将换成得：，

∴ .

则直线的方程为，

即，显然当，.

所以直线经过定点.