题目内容
【题目】已知函数
，
，曲线
在
处的切线方程为
.
（1）求
的解析式；
（2）当时，求证：
；
（3）若
对任意的
恒成立，则实数
的取值范围.
【答案】（1）
（2）见解析(3)
【解析】
（1）由题意利用导函数与原函数的关系得到关于a,b的方程组，求解方程组即可确定函数的解析式；
（2）构造函数φ（x）=f（x）+x2-x=ex-x-1，利用导函数的性质确定其最小值即可证得题中的不等式；
（3）将原问题转化为
≥k对任意的x∈（0，+∞）恒成立，然后构造函数结合(2)中的结论求解实数k的取值范围即可.
（1）f（x）=ex-x2+a，f'（x）=ex-2x．
由已知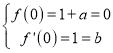
，f（x）=ex-x2-1．
（2）令φ（x）=f（x）+x2-x=ex-x-1，φ'（x）=ex-1，由φ'（x）=0，得x=0，
当x∈（-∞，0）时，φ'（x）＜0，φ（x）单调递减；
当x∈（0，+∞）时，φ'（x）＞0，φ（x）单调递增．
∴φ（x）min=φ（0）=0，从而f（x）≥-x2+x．
（3）f（x）＞kx对任意的x∈（0，+∞）恒成立
≥k对任意的x∈（0，+∞）恒成立，
令g（x）=，x＞0，
∴g′（x）=
，
由（2）可知当x∈（0，+∞）时，ex-x-1＞0恒成立，
令g'（x）＞0，得x＞1；g'（x）＜0，得0＜x＜1．
∴g（x）的增区间为（1，+∞），减区间为（0，1）．g（x）min=g（1）=0．
∴k≤g（x）min=g（1）=e-2，∴实数k的取值范围为（-∞，e-2]．
【题目】某二手交易市场对某型号的二手汽车的使用年数
（
）与销售价格
（单位：万元/辆）进行整理，得到如下的对应数据：
使用年数 | 2 | 4 | 6 | 8 | 10 |
销售价格 | 16 | 13 | 9.5 | 7 | 4.5 |
（I）试求关于的回归直线方程
.
（参考公式：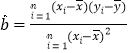
，
）
（II）已知每辆该型号汽车的收购价格为
万元，根据（I）中所求的回归方程，预测为何值时，销售一辆该型号汽车所获得的利润
最大？（利润=销售价格-收购价格）
【题目】《中华人民共和国道路交通安全法》第47条规定：机动车行经人行横道时，应当减速慢行；遇到行人正在通过人行横道，应当停车让行，俗称“礼让斑马线”.下表是某十字路口监控设备所抓拍的6个月内驾驶员不“礼让斑马线”行为的统计数据：
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
不“礼让斑马线”驾驶员人数 | 120 | 105 | 100 | 85 | 90 | 80 |
（Ⅰ）请根据表中所给前5个月的数据，求不“礼让斑马线”的驾驶员人数
与月份
之间的回归直线方程
；
（Ⅱ）若该十字路口某月不“礼让斑马线”驾驶员人数的实际人数与预测人数之差小于5，则称该十字路口“礼让斑马线”情况达到“理想状态”.试根据（Ⅰ）中的回归直线方程，判断6月份该十字路口“礼让斑马线”情况是否达到“理想状态”？
（Ⅲ）若从表中3、4月份分别选取4人和2人，再从所选取的6人中任意抽取2人进行交规调查，求抽取的两人恰好来自同一月份的概率.
参考公式：
，
.
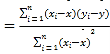