题目内容
【题目】如图:椭圆![]() 的顶点为
的顶点为![]() ,左右焦点分别为
,左右焦点分别为![]() ,
,![]() ,
,![]()

(1)求椭圆![]() 的方程;
的方程;
(2)过右焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,试探究在
两点,试探究在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值?若存在求出点
为定值?若存在求出点![]() 的坐标,若不存在请说明理由?
的坐标,若不存在请说明理由?
【答案】(1)![]() ;(2)在
;(2)在![]() 轴上存在定点
轴上存在定点![]() ,使得
,使得![]() 为定值
为定值
【解析】
(1)根据![]() ,
,![]() 和
和![]() 可构造出关于
可构造出关于![]() 的方程组,求解可得标准方程;(2)当直线斜率不为
的方程组,求解可得标准方程;(2)当直线斜率不为![]() 时,设
时,设![]() ,
,![]() ,
,![]() ,直线
,直线![]() 的方程为
的方程为![]() ,联立直线与椭圆方程,列出
,联立直线与椭圆方程,列出![]() ,代入韦达定理的结果可整理出
,代入韦达定理的结果可整理出![]() ,根据
,根据![]() 可求得
可求得![]() 和
和![]() 的值;当直线斜率为
的值;当直线斜率为![]() 时,可知所求的
时,可知所求的![]() 依然满足
依然满足![]() 是上面所求的值,从而可得结果.
是上面所求的值,从而可得结果.
(1)由![]() 知:
知:![]() ……①
……①
由![]() 知:
知:![]() ,即
,即![]() ……②
……②
又![]() ……③
……③
由①②③得:![]() ,
,![]()
![]() 所求方程为:
所求方程为:![]()
(2)①当直线![]() 的斜率不为
的斜率不为![]() 时
时
设![]() ,
,![]() ,
,![]() ,直线
,直线![]() 的方程为
的方程为![]()
由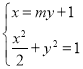 得:
得:![]()
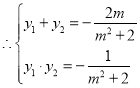
![]()
![]()
![]()
![]()
由![]() ,得:
,得:![]() ,故此时点
,故此时点![]() ,
,![]()
②当直线![]() 的斜率为
的斜率为![]() 时,
时,![]()
综上所述:在![]() 轴上存在定点
轴上存在定点![]() ,使得
,使得![]() 为定值
为定值

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
【题目】《中华人民共和国道路交通安全法》第47条规定:机动车行经人行横道时,应当减速慢行;遇到行人正在通过人行横道,应当停车让行,俗称“礼让斑马线”.下表是某十字路口监控设备所抓拍的6个月内驾驶员不“礼让斑马线”行为的统计数据:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
不“礼让斑马线”驾驶员人数 | 120 | 105 | 100 | 85 | 90 | 80 |
(Ⅰ)请根据表中所给前5个月的数据,求不“礼让斑马线”的驾驶员人数![]() 与月份
与月份![]() 之间的回归直线方程
之间的回归直线方程![]() ;
;
(Ⅱ)若该十字路口某月不“礼让斑马线”驾驶员人数的实际人数与预测人数之差小于5,则称该十字路口“礼让斑马线”情况达到“理想状态”.试根据(Ⅰ)中的回归直线方程,判断6月份该十字路口“礼让斑马线”情况是否达到“理想状态”?
(Ⅲ)若从表中3、4月份分别选取4人和2人,再从所选取的6人中任意抽取2人进行交规调查,求抽取的两人恰好来自同一月份的概率.
参考公式:
 ,
,![]() .
.