题目内容
【题目】如图,在三棱柱![]() 中,
中,![]() 平面ABC,
平面ABC,![]() ,E是BC的中点,
,E是BC的中点,![]() .
.

![]() 求异面直线AE与
求异面直线AE与![]() 所成的角的大小;
所成的角的大小;
![]() 若G为
若G为![]() 中点,求二面角
中点,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)以![]() 分别为
分别为![]() 轴建立空间直角坐标系,利用向量
轴建立空间直角坐标系,利用向量![]() 的夹角公式,求得夹角的余弦值,然后求得夹角的大小.(2)通过计算平面
的夹角公式,求得夹角的余弦值,然后求得夹角的大小.(2)通过计算平面![]() 和平面
和平面![]() 的法向量,利用空间向量夹角公式,计算得二面角的余弦值.
的法向量,利用空间向量夹角公式,计算得二面角的余弦值.
解:![]() 在三棱柱
在三棱柱![]() 中,
中,![]() 平面ABC,
平面ABC,![]() ,
,

E是BC的中点,![]() .
.
以A为原点,AB为x轴,AC为y轴,![]() 为z轴,建立空间直角坐标系,
为z轴,建立空间直角坐标系,
![]() 0,
0,![]() ,
,![]() 0,
0,![]() ,
,![]() 2,
2,![]() ,
,![]() 1,
1,![]() ,
,![]() 0,
0,![]() ,
,
![]() 1,
1,![]() ,
,![]() 2,
2,![]() ,
,
设异面直线AE与![]() 所成的角为
所成的角为![]() ,
,
则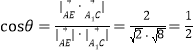 ,
,
![]() ,
,
![]() 异面直线AE与
异面直线AE与![]() 所成的角为
所成的角为![]() .
.
![]() 2,
2,![]() ,
,![]() 2,
2,![]() ,
,
设平面AGE的法向量![]() y,
y,![]() ,
,
则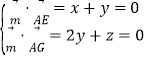 ,取
,取![]() ,得
,得![]() ,
,
平面ACG的法向量![]() 0,
0,![]() ,
,
设二面角![]() 的平面角为
的平面角为![]() ,
,
![]() .
.
![]() 二面角
二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某校进行文科、理科数学成绩对比,某次考试后,各随机抽取100名同学的数学考试成绩进行统计,其频率分布表如下.
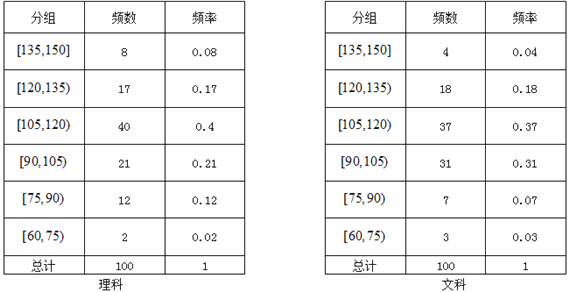
(Ⅰ)根据数学成绩的频率分布表,求理科数学成绩的中位数的估计值;
(Ⅱ)请填写下面的列联表,并根据列联表判断是否有90%的把握认为数学成绩与文理科有关:

(Ⅲ)设文理科数学成绩相互独立,记![]() 表示事件“文科、理科数学成绩都大于等于120分”,估计
表示事件“文科、理科数学成绩都大于等于120分”,估计![]() 的概率.
的概率.
附: 
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |


