题目内容
【题目】已知平面内动点![]() 到两定点
到两定点![]() 和
和![]() 的距离之和为4.
的距离之和为4.
(Ⅰ)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)已知直线![]() 和
和![]() 的倾斜角均为
的倾斜角均为![]() ,直线
,直线![]() 过坐标原点
过坐标原点![]() 且与曲线
且与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,直线
两点,直线![]() 过点
过点![]() 且与曲线
且与曲线![]() 是交于
是交于![]() ,
, ![]() 两点,求证:对任意
两点,求证:对任意![]() ,
, ![]() .
.
【答案】(Ⅰ) ![]() (Ⅱ)见解析
(Ⅱ)见解析
【解析】试题分析:(Ⅰ)由椭圆定义可得动点![]() 的轨迹E是以定点
的轨迹E是以定点![]() 和
和![]() 为焦点的椭圆,且
为焦点的椭圆,且![]() ,从而得方程;
,从而得方程;
(Ⅱ)由题设可设直线![]() 的参数方程分别为
的参数方程分别为![]() ;
; ![]() ,将直线
,将直线![]() 的参数方程分别和椭圆
的参数方程分别和椭圆![]() 联立后整理得:
联立后整理得: ![]() ;
; ![]() ,由
,由![]() 和
和![]() ,从而由韦达定理求解即可.
,从而由韦达定理求解即可.
试题解析:
(Ⅰ)解: ![]() 则根据椭圆的定义得:动点
则根据椭圆的定义得:动点![]() 的轨迹E是以定点
的轨迹E是以定点![]() 和
和![]() 为焦点的椭圆,且
为焦点的椭圆,且![]() ,
,
![]() ,
,
可得动点M的轨迹![]() 的方程为
的方程为![]() .
.
(Ⅱ)证明:由题设可设直线![]() 的参数方程分别为
的参数方程分别为
![]() ;
; ![]() .
.
将直线![]() 的参数方程分别和椭圆
的参数方程分别和椭圆![]() 联立后整理得:
联立后整理得:
![]() ;
; ![]() .
.
则由参数t的几何意义、根与系数的关系及椭圆的对称性有:
![]() ;
;
![]() ,
,
故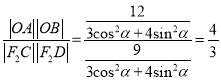 .
.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目



