题目内容
12.边长为a的正六边形的一个顶点为极点,极轴通过它的一边,求正六边形各顶点坐标.分析 直接由极坐标的定义结合正六边形的性质得答案.
解答 解:如图,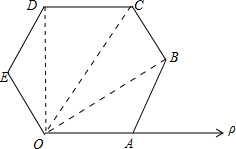
由点的极坐标的定义可知,各点的极坐标分别为:
O(0,0),A(a,0),B($\sqrt{3}a,\frac{π}{6}$),C(2a,$\frac{π}{3}$),D($\sqrt{3}a$,$\frac{π}{2}$),E(a,$\frac{2π}{3}$);
或O(0,0),A(a,0),B($\sqrt{3}a$,-$\frac{π}{6}$),C(2a,-$\frac{π}{3}$),D($\sqrt{3}a$,-$\frac{π}{2}$),E(a,-$\frac{2π}{3}$).
点评 本题考查简单曲线的极坐标方程,考查了极坐标的定义,是基础题.

练习册系列答案
相关题目
2.如果一个复数与它的模的和为5+$\sqrt{3}$i,那么这个复数是( )
| A. | $\frac{11}{5}$ | B. | $\sqrt{3}$ | C. | $\frac{11}{5}$+$\sqrt{3}$i | D. | $\frac{11}{5}$+2$\sqrt{3}$i |
17.已知双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点为F,O坐标原点,以OF直径的圆与双曲线的一条渐近线相交于O,A两点,且|OA|=2|AF|,则双曲线的离心率等于( )
| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\frac{3}{2}$ | D. | $\frac{\sqrt{5}}{2}$ |
1.设公差不为0的等差数列{an}首项a1=9,且a4是a1与a8的等比中项,则公差d=( )
| A. | $\frac{1}{9}$ | B. | 1 | C. | 6 | D. | 9 |
2.已知α=cos234°-cos256°,b=2sin78°sin12°,c=$\frac{2tan12°}{1-ta{n}^{2}12°}$,则有( )
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | c>b>a |
 如图在三棱柱ABC-A1B1C1中,侧面AA1C1C是矩形,且侧面AA1C1C⊥底面AA1B1B,M是AB的中点,若AA1=2,AC=1,∠A1AB=60°,CB1⊥A1B.
如图在三棱柱ABC-A1B1C1中,侧面AA1C1C是矩形,且侧面AA1C1C⊥底面AA1B1B,M是AB的中点,若AA1=2,AC=1,∠A1AB=60°,CB1⊥A1B.