题目内容
1.设公差不为0的等差数列{an}首项a1=9,且a4是a1与a8的等比中项,则公差d=( )| A. | $\frac{1}{9}$ | B. | 1 | C. | 6 | D. | 9 |
分析 解方程(9+3d)2=9•(9+7d)即可.
解答 解:依题意,(9+3d)2=9•(9+7d),
解得:d=1或d=0(舍),
故选:B.
点评 本题考查等差数列的性质,注意解题方法的积累,属于基础题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
6.已知F1,F2是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a,b>0)的左、右焦点,过F1且垂直于x轴的直线与双曲线交于A,B两点,若△ABF2为钝角三角形,则该双曲线的离心率e的取值范围是( )
| A. | (1,+∞) | B. | $(\sqrt{2}+1,+∞)$ | C. | $(1,\sqrt{2}+1)$ | D. | $(1,\sqrt{3})$ |
10.下列说法中,错误的是( )
| A. | 命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0” | |
| B. | 对于命题p:?x∈R,使得x2+x+1<0,则¬p为:?x∈R,均有x2+x+1≥0 | |
| C. | 若p∧q为假命题,则p,q均为假命题 | |
| D. | “x>2”是“x2-3x+2>0”的充分不必要条件 |
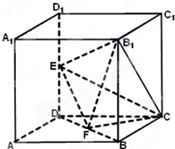 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.