��Ŀ����
ij��˾ȫ�������ΪbԪ������һ������Ϊ����nλְ����������䷽������:���Ƚ�ְ��������ҵ��(����ҵ��������ͬ)�Ӵ�С����1��n����1λְ���ý���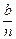 Ԫ��Ȼ���ٽ�������n������2λְ�������˷�����������һ����ÿλְ�����������ʣ�ಿ����Ϊ��˾��չ����.
Ԫ��Ȼ���ٽ�������n������2λְ�������˷�����������һ����ÿλְ�����������ʣ�ಿ����Ϊ��˾��չ����.
(1)��ak(1��k��n)Ϊ��kλְ�����ý��������a2,a3������k��n��b��ʾak(����֤��)��
(2)֤��ak��ak+1(k=1,2,��,n��1),�����ʹ˲���ʽ���ڷ���ԭ���ʵ�����壻
(3)��չ������n��b�йأ���ΪPn(b),�Գ���b����n�仯ʱ����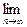 Pn(b).
Pn(b).
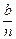 Ԫ��Ȼ���ٽ�������n������2λְ�������˷�����������һ����ÿλְ�����������ʣ�ಿ����Ϊ��˾��չ����.
Ԫ��Ȼ���ٽ�������n������2λְ�������˷�����������һ����ÿλְ�����������ʣ�ಿ����Ϊ��˾��չ����.(1)��ak(1��k��n)Ϊ��kλְ�����ý��������a2,a3������k��n��b��ʾak(����֤��)��
(2)֤��ak��ak+1(k=1,2,��,n��1),�����ʹ˲���ʽ���ڷ���ԭ���ʵ�����壻
(3)��չ������n��b�йأ���ΪPn(b),�Գ���b����n�仯ʱ����
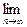 Pn(b).
Pn(b).(1) ak= (1��
(1�� )k��1b; (2) ������䷽�������ˡ����ͷ��䡱���Դ��������ԭ��(3)
)k��1b; (2) ������䷽�������ˡ����ͷ��䡱���Դ��������ԭ��(3) .
.
 (1��
(1�� )k��1b; (2) ������䷽�������ˡ����ͷ��䡱���Դ��������ԭ��(3)
)k��1b; (2) ������䷽�������ˡ����ͷ��䡱���Դ��������ԭ��(3) .
.(1)��1λְ���Ľ���a1= ��
��
��2λְ���Ľ���a2= (1��
(1�� )b��
)b��
��3λְ���Ľ���a3= (1��
(1�� )2b������
)2b������
��kλְ���Ľ���ak= (1��
(1�� )k��1b;
)k��1b;
(2)ak��ak+1= (1��
(1�� )k��1b��0���˽�����䷽�������ˡ����ͷ��䡱���Դ��������ԭ��
)k��1b��0���˽�����䷽�������ˡ����ͷ��䡱���Դ��������ԭ��
(3)��fk(b)��ʾ������kλְ������ʣ������
��f1(b)=(1�� )b,f2(b)=(1��
)b,f2(b)=(1�� )2b,��,fk(b)=(1��
)2b,��,fk(b)=(1�� )kb.
)kb.
��Pn(b)=fn(b)=(1�� )nb,
)nb,
�� .
.
 ��
����2λְ���Ľ���a2=
 (1��
(1�� )b��
)b����3λְ���Ľ���a3=
 (1��
(1�� )2b������
)2b��������kλְ���Ľ���ak=
 (1��
(1�� )k��1b;
)k��1b;(2)ak��ak+1=
 (1��
(1�� )k��1b��0���˽�����䷽�������ˡ����ͷ��䡱���Դ��������ԭ��
)k��1b��0���˽�����䷽�������ˡ����ͷ��䡱���Դ��������ԭ��(3)��fk(b)��ʾ������kλְ������ʣ������
��f1(b)=(1��
 )b,f2(b)=(1��
)b,f2(b)=(1�� )2b,��,fk(b)=(1��
)2b,��,fk(b)=(1�� )kb.
)kb.��Pn(b)=fn(b)=(1��
 )nb,
)nb,��
 .
.
��ϰ��ϵ�д�
�����Ŀ
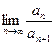 ��
�� )��1.
)��1.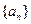 ��ǰ
��ǰ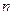 ��Ϊ
��Ϊ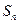 ����֪
����֪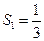 ��
��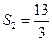 ��
��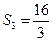 ��
��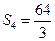 ��
��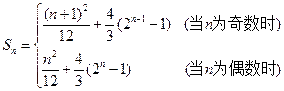 ��
��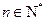 ����
���� 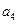 ��������
��������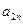 ��������ͣ�
��������ͣ�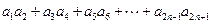 ��
��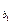 ,a
,a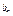 ,��,a
,��,a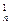 b1+C
b1+C b2+C
b2+C b3+��+C
b3+��+C bn,��
bn,��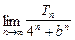 .
.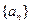 �Ǹ��Ϊ���������У�
�Ǹ��Ϊ���������У�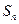 Ϊ��ǰ
Ϊ��ǰ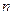 ��ĺͣ���
��ĺͣ���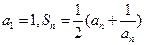
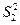 ��
��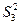 ��ֵ����II��������
��ֵ����II��������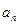 ����III����֤��
����III����֤��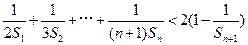
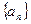 Ϊ�Ȳ����У�
Ϊ�Ȳ����У� ����
����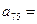
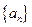 �У���֪
�У���֪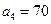 ��
��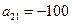 ��
��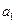 �빫��
�빫��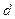 ����д��ͨ�ʽ��
����д��ͨ�ʽ��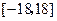 ��
��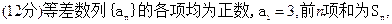
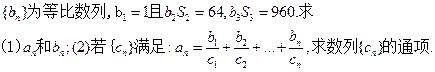
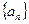 ������Ϊ1���������У���
������Ϊ1���������У���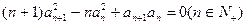 ��
��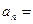 .
.