题目内容
已知数列{an}为等差数列,公差d≠0,由{an}中的部分项组成的数列
a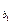 ,a
,a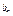 ,…,a
,…,a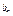 ,…为等比数列,其中b1=1,b2=5,b3=17.
,…为等比数列,其中b1=1,b2=5,b3=17.
(1)求数列{bn}的通项公式;
(2)记Tn=C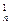 b1+C
b1+C b2+C
b2+C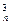 b3+…+C
b3+…+C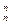 bn,求
bn,求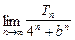 .
.
a
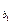 ,a
,a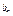 ,…,a
,…,a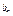 ,…为等比数列,其中b1=1,b2=5,b3=17.
,…为等比数列,其中b1=1,b2=5,b3=17.(1)求数列{bn}的通项公式;
(2)记Tn=C
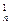 b1+C
b1+C b2+C
b2+C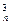 b3+…+C
b3+…+C bn,求
bn,求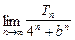 .
.(1) bn=2·3n-1-1 (2)

(1)由题意知a52=a1·a17,即(a1+4d)2=a1(a1+16d)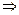 a1d=2d2,
a1d=2d2,
∵d≠0,∴a1=2d,数列{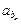 }的公比q=
}的公比q=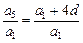 =3,
=3,
∴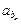 =a1·3n-1 ①
=a1·3n-1 ①
又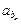 =a1+(bn-1)d=
=a1+(bn-1)d=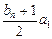 ②
②
由①②得a1·3n-1=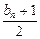 ·a1.∵a1=2d≠0,∴bn=2·3n-1-1.
·a1.∵a1=2d≠0,∴bn=2·3n-1-1.
(2)Tn=C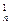 b1+C
b1+C b2+…+C
b2+…+C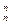 bn
bn
=C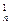 (2·30-1)+C
(2·30-1)+C ·(2·31-1)+…+C
·(2·31-1)+…+C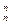 (2·3n-1-1)
(2·3n-1-1)
=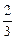 (C
(C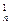 +C
+C ·32+…+C
·32+…+C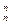 ·3n)-(C
·3n)-(C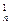 +C
+C +…+C
+…+C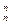 )
)
=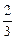 [(1+3)n-1]-(2n-1)=
[(1+3)n-1]-(2n-1)= 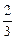 ·4n-2n+
·4n-2n+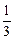 ,
,
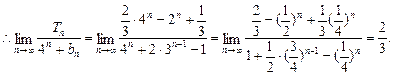
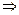 a1d=2d2,
a1d=2d2,∵d≠0,∴a1=2d,数列{
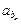 }的公比q=
}的公比q=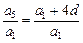 =3,
=3,∴
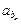 =a1·3n-1 ①
=a1·3n-1 ①又
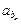 =a1+(bn-1)d=
=a1+(bn-1)d=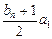 ②
②由①②得a1·3n-1=
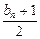 ·a1.∵a1=2d≠0,∴bn=2·3n-1-1.
·a1.∵a1=2d≠0,∴bn=2·3n-1-1.(2)Tn=C
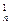 b1+C
b1+C b2+…+C
b2+…+C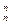 bn
bn=C
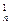 (2·30-1)+C
(2·30-1)+C ·(2·31-1)+…+C
·(2·31-1)+…+C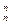 (2·3n-1-1)
(2·3n-1-1)=
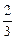 (C
(C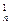 +C
+C ·32+…+C
·32+…+C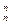 ·3n)-(C
·3n)-(C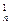 +C
+C +…+C
+…+C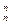 )
)=
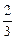 [(1+3)n-1]-(2n-1)=
[(1+3)n-1]-(2n-1)= 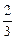 ·4n-2n+
·4n-2n+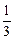 ,
,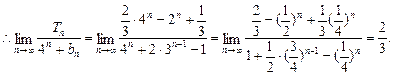

练习册系列答案
相关题目
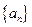 的首项
的首项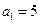 ,前
,前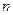 项和为
项和为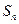 ,且
,且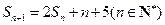 .
.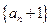 是等比数列;
是等比数列;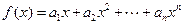 ,求函数
,求函数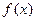 在点
在点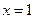 处的导数
处的导数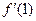 ,并比较
,并比较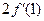 与
与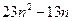 的大小.
的大小.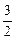 (an-1),数列{bn}的通项公式为bn=4n+3;
(an-1),数列{bn}的通项公式为bn=4n+3;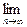
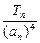

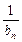 )(其中a>0且a≠1),记Sn是数列{an}的前n项和,试比较Sn与
)(其中a>0且a≠1),记Sn是数列{an}的前n项和,试比较Sn与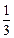 logabn+1的大小,并证明你的结论.
logabn+1的大小,并证明你的结论.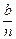 元,然后再将余额除以n发给第2位职工,按此方法将奖金逐一发给每位职工,并将最后剩余部分作为公司发展基金.
元,然后再将余额除以n发给第2位职工,按此方法将奖金逐一发给每位职工,并将最后剩余部分作为公司发展基金.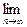 Pn(b).
Pn(b).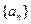 中,
中,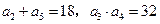 ,并且
,并且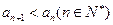 (1)求
(1)求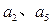 以及数列
以及数列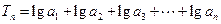 ,求当
,求当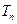 最大时
最大时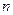 的值.
的值.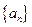 首项
首项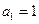 ,前
,前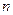 项和
项和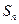 与
与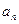 之间满足
之间满足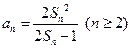
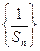 是等差数列 (2)求数列
是等差数列 (2)求数列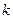 ,使
,使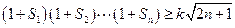 对于一切
对于一切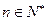 都成立,求
都成立,求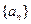 中,
中,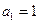 ,
,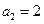 ,且
,且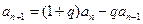 (
(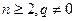 )。
)。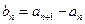 (
(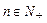 ),求数列
),求数列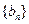 的通项公式;
的通项公式;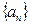 的前n项和为
的前n项和为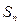 ,对于任意正整数n,都有等式:
,对于任意正整数n,都有等式: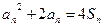 成立,求
成立,求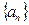 的通项an.
的通项an.