题目内容
函数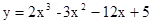 在
在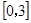 上的最大值和最小值分别是
上的最大值和最小值分别是
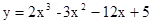 在
在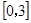 上的最大值和最小值分别是
上的最大值和最小值分别是| A.5,-15 | B.5, -4 | C.-4,-15 | D.5,-16 |
A
试题分析:由题设知y'=6x2-6x-12,令y'>0,解得x>2,或x<-1,
故函数y=2x3-3x2-12x+5在[0,2]上减,在[2,3]上增,
当x=0,y=5;当x=3,y=-4;当x=2,y=-15.
由此得函数y=2x3-3x2-12x+5在[0,3]上的最大值和最小值分别是5,-15;
故答案为 A
点评:解决该试题的关键是对函数求导,利用导数求研究函数y=2x3-3x2-12x+5在[0,3]上的单调性,判断出最大值与最小值位置。

练习册系列答案
相关题目
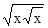 的导数为_______________
的导数为_______________ y=x(x+2)所围成的封闭图形的面积等于
y=x(x+2)所围成的封闭图形的面积等于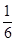
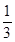
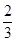
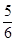
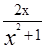 - 2的极值.
- 2的极值.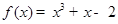 在
在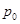 处的切线平行于直线
处的切线平行于直线 ,则
,则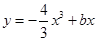 有三个单调区间,则
有三个单调区间,则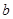 的取值范围是 .
的取值范围是 .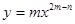 的导数为
的导数为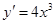 ,则( )
,则( )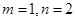
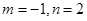
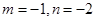
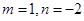
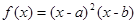 (
( ).
).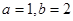 时,求曲线
时,求曲线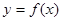 在点
在点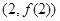 处的切线方程;
处的切线方程; 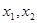 是
是 的两个极值点,
的两个极值点,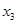 是
是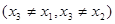 .证明:存在实数
.证明:存在实数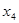 ,使得
,使得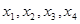 按某种顺序排列后构成等差数列,并求
按某种顺序排列后构成等差数列,并求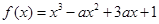 在区间
在区间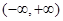 内既有极大值,又有极小值,
内既有极大值,又有极小值, 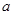 的取值范围是 .
的取值范围是 .