题目内容
一束光线从点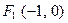 出发,经直线
出发,经直线 上一点
上一点 反射后,恰好穿过点
反射后,恰好穿过点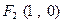 .(Ⅰ)求点
.(Ⅰ)求点 关于直线
关于直线 的对称点
的对称点 的坐标;
的坐标;
(Ⅱ)求以 、
、 为焦点且过点
为焦点且过点 的椭圆
的椭圆 的方程;
的方程;
(Ⅲ)设直线 与椭圆
与椭圆 的两条准线分别交于
的两条准线分别交于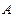 、
、 两点,点
两点,点 为线段
为线段 上的动点,求点
上的动点,求点 到
到 的距离与到椭圆
的距离与到椭圆 右准线的距离之比的最小值,并求取得最小值时点
右准线的距离之比的最小值,并求取得最小值时点 的坐标.
的坐标.
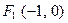 出发,经直线
出发,经直线 上一点
上一点 反射后,恰好穿过点
反射后,恰好穿过点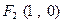 .(Ⅰ)求点
.(Ⅰ)求点 关于直线
关于直线 的对称点
的对称点 的坐标;
的坐标;(Ⅱ)求以
 、
、 为焦点且过点
为焦点且过点 的椭圆
的椭圆 的方程;
的方程;(Ⅲ)设直线
 与椭圆
与椭圆 的两条准线分别交于
的两条准线分别交于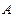 、
、 两点,点
两点,点 为线段
为线段 上的动点,求点
上的动点,求点 到
到 的距离与到椭圆
的距离与到椭圆 右准线的距离之比的最小值,并求取得最小值时点
右准线的距离之比的最小值,并求取得最小值时点 的坐标.
的坐标.(Ⅰ)
 的坐标为
的坐标为 .
.(Ⅱ)所求椭圆方程为
 .
.(Ⅲ)
 最小值=
最小值= ,此时点
,此时点 的坐标为
的坐标为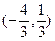
(Ⅰ)设
 的坐标为
的坐标为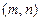 ,则
,则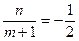 且
且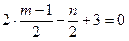 .
.解得
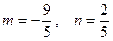 , 因此,点
, 因此,点 的坐标为
的坐标为 .
.(Ⅱ)
 ,根据椭圆定义,
,根据椭圆定义,得

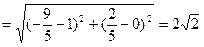 ,
, ,
, . ∴所求椭圆方程为
. ∴所求椭圆方程为 .
.(Ⅲ)
 ,
, 椭圆的准线方程为
椭圆的准线方程为 .
. 设点
 的坐标为
的坐标为
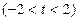 ,
, 表示点
表示点 到
到 的距离,
的距离,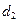 表示点
表示点 到椭圆的右准线的距离.
到椭圆的右准线的距离.则
 ,
, .
.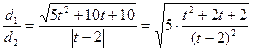 ,令
,令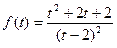
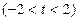 ,则
,则 ,
,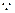 当
当 ,
,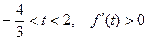 ,
,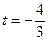 ,
,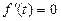 .
.∴
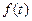 在
在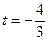 时取得最小值.
时取得最小值.因此,
 最小值=
最小值= ,此时点
,此时点 的坐标为
的坐标为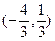 -----------------14分
-----------------14分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 过点(1,
过点(1,  ),F1、F2分别为其左、右焦点,且离心率e=
),F1、F2分别为其左、右焦点,且离心率e= 的直线
的直线 与椭圆C交于不同的两点
与椭圆C交于不同的两点 、
、 ,且∠
,且∠ 为锐角(其中
为锐角(其中 为坐标原点),求直线
为坐标原点),求直线 的取值范围.
的取值范围.  ;
; ,经过定点
,经过定点 且方向向量为
且方向向量为 的直线与经过定点
的直线与经过定点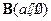 且方向向量为
且方向向量为 的直线交于点M,其中
的直线交于点M,其中 R,常数a>0.
R,常数a>0. ,过点
,过点 的直线与点M的轨迹交于C、D两点,求
的直线与点M的轨迹交于C、D两点,求 的取值范围.
的取值范围. 的离心率
的离心率 ,
,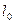 为过点
为过点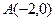 和上顶点
和上顶点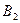 的直线,下顶点
的直线,下顶点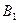 与
与 .
. 交
交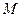 , 若
, 若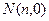 ,试求
,试求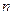 的范围.
的范围.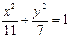 上一点到直线
上一点到直线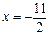 与到点(-2,0)的距离之比为
与到点(-2,0)的距离之比为 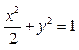 ,
,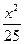 +
+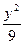 ="1"
="1"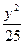 +
+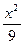 =1(y≠0)
=1(y≠0)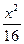 +
+ +
+ =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,左焦点为F,A、B、C为其三个顶点,直线CF与AB交于D,则tan∠BDC的值等于( )
,左焦点为F,A、B、C为其三个顶点,直线CF与AB交于D,则tan∠BDC的值等于( )
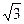 B.-3
B.-3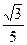 D.-
D.-