题目内容
【题目】已知函数f（x）=|x2﹣1|+x2+kx．
（1）若对于区间（0，+∞）内的任意x，总有f（x）≥0成立，求实数k的取值范围；
（2）若函数f（x）在区间（0，2）内有两个不同的零点x1 ， x2 ， 求：
①实数k的取值范围；
② 
的取值范围．
【答案】
（1）解：f（x）≥0|x2﹣1|+x2+kx≥0k≥﹣ 
，x∈（0，+∞），
记g（x）=﹣ = 
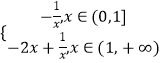，易知g（x）在（0，1]上递增，在（1，+∞）上递减，
∴g（x）max=g（1）=﹣1，
∴k≥﹣1；
（2）解：①（ⅰ）0＜x≤1时，方程f（x）=0化为kx+1=0，k=0时，无解；k≠0时，x=﹣ 
；
（ⅱ）1＜x＜2时，方程f（x）=0化为2x2+kx﹣1=0，x= 
，而其中 
＜ 
≤0，
故f（x）=0在区间（1，2）内至多有一解x= 
；
综合（ⅰ）（ⅱ）可知，k≠0，且0＜x≤1时，方程f（x）=0有一解x=﹣ ，故k≤﹣1；
1＜x＜2时，方程f（x）=0也仅有一解x= ，令1＜ ＜2，得﹣ 
＜k＜﹣1，
∴实数k的取值范围是﹣ ＜k＜﹣1；
②方程f（x）=0的两解分别为x1=﹣ ，x2= ，
=﹣k+ 
=﹣k+ 
= =2x2∈（2，4）．
【解析】（1）由f（x）≥0分离出参数k，得k≥﹣ ，x∈（0，+∞），记g（x）=﹣ ，则问题等价于k≥g（x）max ， 由单调性可得g（x）max；（2）①（i）当0＜x≤1时，方程f（x）=0为一次型方程，易判断k≠0时有一解；当1＜x＜2时，方程f（x）=0为二次方程，可求得两解，易判断其一不适合，令另一解大于1小于2，可得k的范围，综合可得结论；（ii）由①易知两零点x1 ， x2 ， 从而可表示出 ，化简可得为2x2 ， 结合（ii）可得结论；
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案【题目】为了增强环保意识，我校从男生中随机抽取了60人，从女生中随机抽取了50人参加环保知识测试，统计数据如下表所示：
优秀 | 非优秀 | 总计 | |
男生 | 40 | 20 | 60 |
女生 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
（1）试判断是否有99%的把握认为环保知识是否优秀与性别有关；
（2）为参加市里举办的环保知识竞赛，学校举办预选赛，已知在环保测试中优秀的同学通过预选赛的概率为 
，现在环保测试中优秀的同学中选3人参加预选赛，若随机变量X表示这3人中通过预选赛的人数，求X的分布列与数学期望．
附：K2= 
P（K2≥k） | 0.500 | 0.400 | 0.100 | 0.010 | 0.001 |
k | 0.455 | 0.708 | 2.706 | 6.635 | 10.828 |
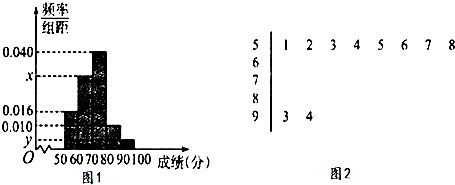
【题目】《中华人民共和国道路交通安全法》规定：车辆驾驶员血液酒精浓度在20～80mg/100mL（不含80）之间，属于酒后驾车；在80mg/100mL（含80）以上时，属于醉酒驾车．某市公安局交通管理部门在某路段的一次拦查行动中，依法检查了300辆机动车，查处酒后驾车和醉酒驾车的驾驶员共20人，检测结果如表：
酒精含量（mg/100mL） | [20，30） | [30，40） | [40，50） | [50，60） | [60，70） | [70，80） | [80，90） | [90，100） |
人数 | 3 | 4 | 1 | 4 | 2 | 3 | 2 | 1 |
（1）绘制出检测数据的频率分布直方图（计算并标上选取的y轴单位长度，在图中用实线画出矩形框并用阴影表示），估计检测数据中酒精含量的众数
（2）求检测数据中醉酒驾驶的频率，并估计检测数据中酒精含量的中位数、平均数（请写出计算过程）．
