题目内容
【题目】已知二次函数f(x)=x2+bx+c(其中b,c为实常数).
(1)若b>2,且y=f(sinx)(x∈R)的最大值为5,最小值为﹣1,求函数y=f(x)的解析式;
(2)是否存在这样的函数y=f(x),使得{y|y=x2+bx+c,﹣1≤x≤0}=[﹣1,0],若存在,求出函数y=f(x)的解析式;若不存在,请说明理由.
(3)记集合A={x|f(x)=x,x∈R},B={x|f(f(x))=x,x∈R}.
①若A≠,求证:B≠;
②若A=,判断B是否也为空集.
【答案】
(1)解:由条件知f(x)=x2+bx+c的最大值为5,最小值为﹣1
而b>2,则对称轴 ![]() ,
,
则 ![]() ,即
,即 ![]() ,
,
解得 ![]()
则f(x)=x2+3x+1.
(2)解:f(x)=x2+bx+c,﹣1≤x≤0,对称轴x=﹣ ![]() ,
,
若b≥2,则 ![]() ,则
,则 ![]() ,
,
解得 ![]() ,此时f(x)=x2+2x,
,此时f(x)=x2+2x,
若b≤0,则 ![]() ,则
,则 ![]() ,
,
解得 ![]() ,此时f(x)=x2﹣1,
,此时f(x)=x2﹣1,
若0<b≤1,则 ![]() ,则
,则 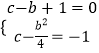 ,
,
解得 ![]() (舍)或
(舍)或 ![]() (舍),
(舍),
此时不存在函数f(x),若1<b<2,则 ![]() ,
,
则 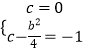 ,解得
,解得 ![]() (舍)或
(舍)或 ![]() (舍),此时不存在函数f(x),
(舍),此时不存在函数f(x),
综上所述存在函数f(x)=x2﹣1和f(x)=x2+2x满足条件
(3)解:由f(x)=x2+bx+c得f(f(x))=f2(x)+bf(x)+c及c=f(x)﹣x2﹣bx,
由f(f(x))=x得到f2(x)+bf(x)+c=x,即f2(x)+bf(x)+f(x)﹣x2﹣bx=x,
整理得到f2(x)﹣x2+b(f(x)﹣x)+(f(x)﹣x)=0,
即(f(x)﹣x)(f(x)+x+b+1)=0①
即f(x)﹣x=0或f(x)+x+b+1=0,
即x2+(b﹣1)x+c=0②或x2+(b+1)x+b+c+1=0③
方程②的判别式△=(b﹣1)2﹣4c
方程③的判别式 ![]() ,
,
①若A≠,即f(x)﹣x=0有解,即x2+(b﹣1)x+c=0有解,即△≥0,则①有解,
即B≠,
②若A=,即△<0,则△1<0,②和③均无解,则①无解,即B=.
【解析】(1)求出函数的对称轴小于﹣1,得到关于b,c的方程组,解出即可;(2)求出f(x)的对称轴,通过讨论对称轴的位置,结合函数的值域求出b,c的值,从而求出f(x)的表达式即可;(3)通过整理方程得到x2+(b﹣1)x+c=0或x2+(b+1)x+b+c+1=0,结合二次函数的性质进行证明即可.
【考点精析】利用二次函数的性质对题目进行判断即可得到答案,需要熟知当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减.
上递减.

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案