题目内容
【题目】(1)求证:椭圆![]() 中斜率为
中斜率为![]() 的平行弦的中点轨迹必过椭圆中心;
的平行弦的中点轨迹必过椭圆中心;
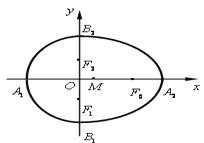
(2)用作图方法找出下面给定椭圆的中心;
(3)我们把由半椭圆![]()
![]() 与半椭圆
与半椭圆![]()
![]() 合成的曲线称作“果圆”,其中
合成的曲线称作“果圆”,其中![]() ,
,![]() ,
,![]() .如图,设点
.如图,设点![]() ,
,![]() ,
,![]() 是相应椭圆的焦点,
是相应椭圆的焦点,![]() ,
,![]() 和
和![]() ,
,![]() 是“果圆” 与
是“果圆” 与![]() ,
,![]() 轴的交点. 连结“果圆”上任意两点的线段称为“果圆”的弦.试研究:是否存在实数
轴的交点. 连结“果圆”上任意两点的线段称为“果圆”的弦.试研究:是否存在实数![]() ,使斜率为
,使斜率为![]() 的“果圆”平行弦的中点轨迹总是落在某个椭圆上?若存在,求出所有可能的
的“果圆”平行弦的中点轨迹总是落在某个椭圆上?若存在,求出所有可能的![]() 值,若不存在,说明理由.
值,若不存在,说明理由.
【答案】(1)证明见解析;(2)作图见解析;(3)存在,![]()
【解析】
(1)根据点差法可求出平行弦的中点的轨迹方程为![]() ,显然直线经过椭圆中心原点;
,显然直线经过椭圆中心原点;
(2)由(1)知,平行弦的中点轨迹必过椭圆中心,所以作出两组平行弦的中点轨迹所在直线,两条直线的交点即为椭圆的中心;
(3)由(1)的结论可知,![]() .设出直线
.设出直线![]() 和弦的中点坐标,即可求得中点所在的轨迹方程为椭圆方程.当
和弦的中点坐标,即可求得中点所在的轨迹方程为椭圆方程.当![]() 或
或![]() 时,平行弦的轨迹可以在直线上,不总在椭圆上.
时,平行弦的轨迹可以在直线上,不总在椭圆上.
(1)证明:设斜率为![]() 的直线与椭圆交于点
的直线与椭圆交于点![]() 两点,
两点,![]() .
.
![]() 中点坐标为
中点坐标为![]() ,所以
,所以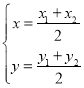 ,
,![]()
所以![]() ,
,![]() ,作差得,
,作差得,![]() ,
,
即有![]() ,即
,即![]() ,再根据中点在椭圆内部,所以
,再根据中点在椭圆内部,所以![]() ,即
,即
![]() ,解得
,解得![]() .
.
故平行弦的中点的轨迹方程为![]() ,
,![]() ,
,
所以椭圆![]() 中斜率为
中斜率为![]() 的平行弦的中点轨迹过椭圆中心.
的平行弦的中点轨迹过椭圆中心.
(2)如图所示,点![]() 即为椭圆中心.
即为椭圆中心.

(3)由(1)的结论可知,![]() .
.
设![]() 交“果圆”于
交“果圆”于![]() 两点,中点为
两点,中点为![]() ,则
,则![]() ,
,![]() ,则
,则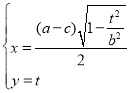 ,即
,即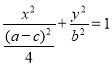 .
.
易证![]() ,
,
当![]() 或
或![]() 时,“果圆”的平行弦的轨迹可以在直线上,不总在椭圆上.
时,“果圆”的平行弦的轨迹可以在直线上,不总在椭圆上.
所以,当![]() 时,“果圆”的平行弦的中点轨迹总是落在某个椭圆上.
时,“果圆”的平行弦的中点轨迹总是落在某个椭圆上.

【题目】某校在高二年级学生中,对自然科学类、社会科学类校本选修课程的选课意向进行调查.现从高二年级学生中随机抽取180名学生,其中男生105名;在这180名学生中选择社会科学类的男生、女生均为45名.
(1)根据抽取的180名学生的调查结果,完成下面的2×2列联表.
(2)判断能否在犯错误的概率不超过0.025的前提下认为科类的选择与性别有关?
选择自然科学类 | 选择社会科学类 | 合计 | |
男生 | |||
女生 | |||
合计 |
参考公式:![]() ,其中
,其中![]() .
.
P(K2≥k0) | 0.500 | 0.400 | 0.250 | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 | |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】空气质量指数AQI是一种反映和评价空气质量的方法,AQI指数与空气质量对应如表所示:
AQI | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | 300以上 |
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
如图是某城市2018年12月全月的AQI指数变化统计图:

根据统计图判断,下列结论正确的是( )
A. 整体上看,这个月的空气质量越来越差
B. 整体上看,前半月的空气质量好于后半个月的空气质量
C. 从AQI数据看,前半月的方差大于后半月的方差
D. 从AQI数据看,前半月的平均值小于后半月的平均值