题目内容
18．已知随机变量X服从正态分布N（1，σ2），若P（X≤2）=0.72，则P（X≤0）=（ ）| A． | 0.22 | B． | 0.28 | C． | 0.36 | D． | 0.64 |
分析 随机变量ξ服从正态分布N（1，σ2），得到曲线关于x=1对称，根据曲线的对称性得到小于等于0的概率和大于等于2的概率是相等的，从而做出大于2的数据的概率，根据概率的性质得到结果．
解答 解：随机变量ξ服从正态分布N（1，σ2），
∴曲线关于x=1对称，
∴P（x≤0）=P（x≥2）=1-P（x≤2）=0.28
故选：B．
点评 本题主要考查正态分布曲线的特点及曲线所表示的意义、函数图象对称性的应用等基础知识，属于基础题．
练习册系列答案
王后雄学案教材完全解读系列答案
海淀课时新作业金榜卷系列答案
相关题目
甲、乙两人在9天每天加工零件的个数用茎叶图表示如图，则这9天甲、乙加工零件个数的中位数之和为91．（考点：茎叶图与中位数综合）
6．已知F1、F2为椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{169}$=1的两个焦点，过F1的直线交椭圆于A、B两点．若|F2A|+|F2B|=30，则|AB|=（ ）
| A． | 16 | B． | 18 | C． | 22 | D． | 20 |
3．执行如图的程序框图，若输出的k=2，则输入x的取值范围是（ ）
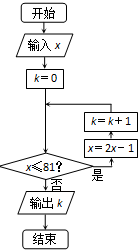
| A． | （21，41） | B． | [21，41] | C． | （21，41] | D． | [21，41） |
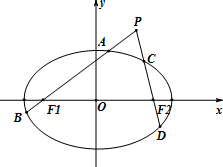如图，已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左右焦点分别为F1，F2，离心率为$\frac{{\sqrt{2}}}{2}$，它的四个顶点连成的菱形的面积为8$\sqrt{2}$．过动点P（不在x轴上）的直线PF1，PF2与椭圆的交点分别为A，B和C，D．