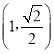Question

【题目】已知定义在R上的偶函数f（x）在（﹣∞，0]上单调递增，且f（﹣1）＝﹣1.若f（x﹣1）+1≥0，则x的取值范围是_____；设函数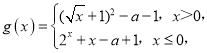若方程f（g（x））+1＝0有且只有两个不同的实数解，则实数a的取值范围为_____.

Answer 1

【答案】[0，2] （﹣∞，﹣1]∪（3，+∞）.

【解析】

根据f（x）的奇偶性和单调性列不等式求出x的范围，根据g（x）的单调性和最值，分情况讨论最值和±1的关系，从而确定a的范围.

由f（x）是偶函数，且f（x）在上单调递增，

所以f（x）在（0，+∞）上单调递减，且f（1）＝f（﹣1）＝﹣1，

由f（x﹣1）+1≥0可得：f（x﹣1）≥f（1），

所以﹣1≤x﹣1≤1，即0≤x≤2.

由f（g（x））+1＝0可得g（x）＝1或g（x）＝﹣1.

由函数解析式可知g（x）在（﹣∞，0]和（0，+∞）上均为增函数，

故当x∈（﹣∞，0]时，g（x）≤2﹣a，当x∈（0，+∞）时，g（x）＞﹣a，

（1）若1＞2﹣a＞﹣1＞﹣a，则g（x）＝1有1解，g（x）＝﹣1有2解，不符合题意；

（2）若2﹣a＞1＞﹣a＞﹣1，此时g（x）＝1有2解，g（x）＝﹣1有1解，不符合题意；

（3）若﹣a≥1，则g（x）＝1有1解，g（x）＝﹣1有1解，符合题意；

（4）若2﹣a＜﹣1，则g（x）＝1有1解，g（x）＝﹣1有1解，符合题意；

（5）若2﹣a＝1，则g（x）＝1有2解，g（x）＝﹣1有1解，不符合题意；

（6）若2﹣a＝﹣1，则g（x）＝﹣1有2解，g（x）＝1有1解，不符合题意；

综上，﹣a≥1或2﹣a＜﹣1，解得a≤﹣1或a＞3.

故答案为：[0，2]，（﹣∞，﹣1]∪（3，+∞）.