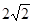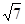题目内容
已知直角坐标系中圆 方程为
方程为 ,
, 为圆内一点(非圆心),
为圆内一点(非圆心),
那么方程 所表示的曲线是———————— ( )
所表示的曲线是———————— ( )
 方程为
方程为 ,
, 为圆内一点(非圆心),
为圆内一点(非圆心),那么方程
 所表示的曲线是———————— ( )
所表示的曲线是———————— ( )A.圆 |
B.比圆 半径小,与圆 半径小,与圆 同心的圆 同心的圆 |
C.比圆 半径大与圆 半径大与圆 同心的圆 同心的圆 |
| D.不一定存在 |
B
试题分析:设圆的一般式方程为:x2+y2+Dx+Ey+F=0(
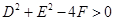 ),因为
),因为 为圆内一点,所以x02+y02+Dx0+Ey0+F<0,所以x2+y2+Dx+Ey+F=x02+y02+Dx0+Ey0+F所表示的曲线是比圆
为圆内一点,所以x02+y02+Dx0+Ey0+F<0,所以x2+y2+Dx+Ey+F=x02+y02+Dx0+Ey0+F所表示的曲线是比圆 半径小,与圆
半径小,与圆 同心的圆。
同心的圆。点评:方程x2+y2+Dx+Ey+F=0,当
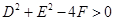 时,表示圆的方程;当
时,表示圆的方程;当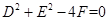 时,表示点
时,表示点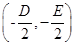 ;当
;当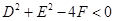 时,不表示任何图形。
时,不表示任何图形。
练习册系列答案
相关题目
 ,
,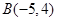 ,则以线段
,则以线段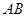 为直径的圆的方程是 .
为直径的圆的方程是 .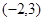 为圆心且与y轴相切的圆的方程是 .
为圆心且与y轴相切的圆的方程是 . 与圆
与圆 的两个交点,则
的两个交点,则 ( )
( ) D.
D.
 则满足条件的查找的条数是____________。
则满足条件的查找的条数是____________。 与椭圆
与椭圆 交于
交于 两点,以线段
两点,以线段 为直径的圆过椭圆的右焦点,则椭圆
为直径的圆过椭圆的右焦点,则椭圆 的离心率为( )
的离心率为( )



 上,则点(m,c)不满足下列哪个方程( )
上,则点(m,c)不满足下列哪个方程( )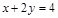


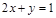
 上有且只有两个点到直线
上有且只有两个点到直线 的距离为1,则半径
的距离为1,则半径 的取值范围是 .
的取值范围是 .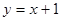 上的一点向圆
上的一点向圆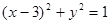 引切线,则切线长的最小值为( )
引切线,则切线长的最小值为( )