题目内容
3.点P是单位圆O外任意一点,过P点作圆O的两条切线,切点为A、B,则$\overrightarrow{PA}•\overrightarrow{PB}$的最小值为$2\sqrt{2}-3$.分析 如图所示,不妨取P(m,0),A(cosθ,sinθ),B(cosθ,-sinθ).(θ∈(0,π)).由于$\overrightarrow{OA}$⊥$\overrightarrow{PA}$,可得$\overrightarrow{OA}$•$\overrightarrow{PA}$=0,得到cosθ=$\frac{1}{m}$.于是$\overrightarrow{PA}•\overrightarrow{PB}$=${m}^{2}+\frac{2}{{m}^{2}}$-3,再利用基本不等式即可得出.
解答 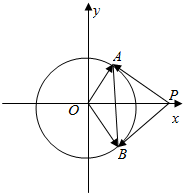 解:如图所示,不妨取P(m,0),A(cosθ,sinθ),B(cosθ,-sinθ).(θ∈(0,π)).
解:如图所示,不妨取P(m,0),A(cosθ,sinθ),B(cosθ,-sinθ).(θ∈(0,π)).
∵$\overrightarrow{OA}$⊥$\overrightarrow{PA}$,
∴$\overrightarrow{OA}$•$\overrightarrow{PA}$=(cosθ,sinθ)•(cosθ-m,sinθ)=cosθ(cosθ-m)+sin2θ=0,
化为cosθ=$\frac{1}{m}$.
∴$\overrightarrow{PA}•\overrightarrow{PB}$=(cosθ-m,sinθ)•(cosθ-m,-sinθ)
=(cosθ-m)2-sin2θ
=2cos2θ+m2-3
=${m}^{2}+\frac{2}{{m}^{2}}$-3≥2$\sqrt{2}$-3,当且仅当m2=$\sqrt{2}$时取等号.
∴$\overrightarrow{PA}•\overrightarrow{PB}$的最小值为2$\sqrt{2}$-3.
故答案为:2$\sqrt{2}$-3.
点评 本题考查了直线与圆相切的性质、数量积的运算、基本不等式的性质等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案| A. | y=2x | B. | y=log2x | C. | y=$\frac{2}{x}$ | D. | y=-2x |
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
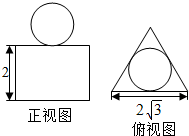 如图一个几何体的正视图和俯视图如图所示,其中俯视图为边长为2$\sqrt{3}$的正三角形,且圆与三角形内切,则该几何体的体积为$6\sqrt{3}+\frac{4π}{3}$.
如图一个几何体的正视图和俯视图如图所示,其中俯视图为边长为2$\sqrt{3}$的正三角形,且圆与三角形内切,则该几何体的体积为$6\sqrt{3}+\frac{4π}{3}$.