题目内容
1.已知函数y=f(x)与y=($\frac{1}{2}$)x的图象关于直线y=x对称,则f(x2-2x-3)的单调递增区间为(-∞,-1).分析 函数y=f(x)与y=($\frac{1}{2}$)x的图象关于直线y=x对称,可得f(x)=$lo{g}_{\frac{1}{2}}x$.利用二次函数、对数函数、复合函数的单调性即可得出.
解答 解:∵函数y=f(x)与y=($\frac{1}{2}$)x的图象关于直线y=x对称,
∴f(x)=$lo{g}_{\frac{1}{2}}x$.
∴f(x2-2x-3)=$lo{g}_{\frac{1}{2}}({x}^{2}-2x-3)$,
由x2-2x-3>0,解得x>3或x<-1.
x2-2x-3=(x-1)2-4,
∴f(x2-2x-3)的单调递增区间为(-∞,-1),
故答案为:(-∞,-1).
点评 本题考查了反函数的求法、二次函数、对数函数、复合函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
9.已知R为实数集,M=$\left\{{y\left|{y=\sqrt{1+x}}\right.}\right\}$,$N=\left\{{x|y=\sqrt{x-1}}\right\}$,则M∩(∁RN)=( )
| A. | {x|0≤x<1} | B. | {x|-1≤x<1} | C. | {x|-1≤x≤0} | D. | {x|0≤x≤1} |
16.若$sinα=-\frac{5}{13},且α$为第四象限角,则$tan({α+\frac{π}{4}})$的值等于( )
| A. | $\frac{7}{17}$ | B. | $\frac{17}{7}$ | C. | $-\frac{5}{12}$ | D. | $\frac{10}{17}$ |
10.下列函数中,值域为(0,+∞)的是( )
| A. | y=-5x | B. | $y={(\frac{1}{3})^{1-x}}$ | ||
| C. | y=x2-2x+3,x∈(-∞,2] | D. | $y=\frac{1}{x+1},x∈[0,+∞)$ |
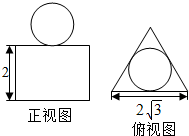 如图一个几何体的正视图和俯视图如图所示,其中俯视图为边长为2$\sqrt{3}$的正三角形,且圆与三角形内切,则该几何体的体积为$6\sqrt{3}+\frac{4π}{3}$.
如图一个几何体的正视图和俯视图如图所示,其中俯视图为边长为2$\sqrt{3}$的正三角形,且圆与三角形内切,则该几何体的体积为$6\sqrt{3}+\frac{4π}{3}$.