题目内容
【题目】如图，在四棱锥P－ABCD中，PA⊥平面ABCD，AB⊥AD，，AC＝AD＝CD，E是AD的中点．
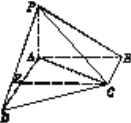
(Ⅰ)证明CE∥平面PAB；
(Ⅱ)证明：平面PAD⊥平面PCE.
【答案】(Ⅰ)见解析(Ⅱ)见解析
【解析】试题分析：（1）
且
，通过证明
来证明CE∥平面PAB。（2）通过证明CE⊥平面PAD，可以证明平面PAD⊥平面PCE.
试题解析：(Ⅰ)证明：∵AC＝AD＝CD，E是AD的中点，
∴CE⊥AD，又在平面ABCD内AB⊥AD，∴AB∥CE
∵CE平面PAB，AB平面PAB ∴CE∥平面PAB.
(Ⅱ)证明：∵PA⊥平面ABCD ，CE平面ABCD，∴PA⊥CE.
∵AC＝AD＝CD，E是AD中点，∴AD⊥CE.
∵PA∩AD＝A，∴CE⊥平面PAD，
∵CE平面PCE ∴平面PAD⊥平面 PCE.
练习册系列答案
相关题目
【题目】已知函数f(x)＝
sinωxcosωx－cos2ωx＋
(ω＞0)，经化简后利用“五点法”画其在某一周期内的图象时，列表并填入的部分数据如下表：
x | ① |
|
| ||
f(x) | 0 | 1 | 0 | －1 | 0 |
(1)请直接写出①处应填的值，并求函数f(x)在区间
上的值域；
(2)△ABC的内角A，B，C所对的边分别为a，b，c，已知f(A＋
)＝1，b＋c＝4，a＝
，求△ABC的面积．
