题目内容
【题目】已知椭圆C: ![]() 的左、右焦点为F1,F2,设点F1,F2与椭圆短轴的一个端点构成斜边长为4的直角三角形.
的左、右焦点为F1,F2,设点F1,F2与椭圆短轴的一个端点构成斜边长为4的直角三角形.
(1)求椭圆C的标准方程;
(2)设A,B,P为椭圆C上三点,满足![]() ,记线段AB中点Q的轨迹为E,若直线l:y=x+1与轨迹E交于M,N两点,求|MN|.
,记线段AB中点Q的轨迹为E,若直线l:y=x+1与轨迹E交于M,N两点,求|MN|.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:
(1)由题意可得![]() ,即可求出
,即可求出![]() ,即可求出椭圆的标准方程;
,即可求出椭圆的标准方程;
(2)方法一:设![]() ,利用向量
,利用向量![]() ,求得点
,求得点![]() 的坐标,根据点
的坐标,根据点![]() 在椭圆上,把直线的方程和椭圆方程,利用根与系数的关系、韦达定理,利用弦长公式,即可求解;
在椭圆上,把直线的方程和椭圆方程,利用根与系数的关系、韦达定理,利用弦长公式,即可求解;
方法二:设![]() ,根据题意和点
,根据题意和点![]() 在椭圆上,化简整理可得
在椭圆上,化简整理可得![]() ,再根据中点坐标公式,消去
,再根据中点坐标公式,消去![]() 线段
线段![]() 的中点
的中点![]() 的轨迹方程,再设
的轨迹方程,再设![]() 两点点坐标为
两点点坐标为![]() ,根据弦长公式即可求出.
,根据弦长公式即可求出.
试题解析:
(1)由已知得2c=4,b=2,故c=2,a=2![]() .
.
故椭圆C的标准方程为![]() +
+![]() =1.
=1.
(2)法一 设A(x1,y1),B(x2,y2),∵![]() =
=![]()
![]() +
+![]()
![]() ,∴
,∴![]() =
=![]() ,故点P坐标为
,故点P坐标为![]() .
.
由于点P在椭圆C上,
故有![]()
![]()
![]() +
+![]()
![]()
![]() =1,
=1,
![]()
![]() +
+![]()
![]() +
+![]()
![]() =1,
=1,
即![]() +
+![]() +
+![]()
![]() =1,即
=1,即![]() +
+![]() =0.
=0.
令线段AB的中点坐标为Q(x,y),则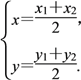
因A,B在椭圆C上,故有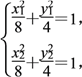
相加有![]() +
+![]() =2.
=2.
故![]() +
+![]() =2,
=2,
由于![]() +
+![]() =0,
=0,
故![]() +
+![]() =2,即Q点的轨迹E的方程为
=2,即Q点的轨迹E的方程为![]() +
+![]() =1.
=1.
联立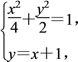 得3x2+4x-2=0.
得3x2+4x-2=0.
设M(x3,y3),N(x4,y4),
则x3+x4=-![]() ,
,
x3·x4=-![]() .
.
故|MN|=![]() |x3-x4|=
|x3-x4|=![]()
![]() =
=![]() .
.
法二 设A(2![]() cos α,2sin α),B(2
cos α,2sin α),B(2![]() cos β,2sin β),
cos β,2sin β),
∵![]() =
=![]()
![]() +
+![]()
![]() ,
,
∴![]() =
=![]() ,故点P坐标为
,故点P坐标为![]() .
.
∵点P在椭圆上,
∴(3cos α+4cos β)2+(3sin α+4sin β)2=25,
∴cos αcos β+sin αsin β=0,∴cos(α-β)=0,
∴α-β=![]() ,
,
∴B(2![]() sin α,-2cos α),
sin α,-2cos α),
∴AB中点Q的坐标为(![]() cos α+
cos α+![]() sin α,sin α-cos α),
sin α,sin α-cos α),
设Q的点坐标为(x,y),
∴x=![]() cos α+
cos α+![]() sin α,y=sin α-cos α,
sin α,y=sin α-cos α,
∴![]() =cos2α+2cos αsin α+sin2α=1+2cos αsin α,
=cos2α+2cos αsin α+sin2α=1+2cos αsin α,
y2=cos2α-2cos αsin α+sin2α=1-2cos αsin α,
∴![]() +y2=2,
+y2=2,
即线段AB中点Q的轨迹为E的方程为![]() +
+![]() =1.
=1.
设M,N两点的坐标为(x1,y1),(x2,y2),
由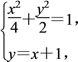 消y,
消y,
整理得3x2+4x-2=0,
∴x1+x2=-![]() ,x1x2=-
,x1x2=-![]() ,
,
∴|MN|=![]() |x1-x2|=
|x1-x2|=![]() ×
×![]() =
=![]() .
.

【题目】已知函数f(x)=![]() sinωxcosωx-cos2ωx+
sinωxcosωx-cos2ωx+![]() (ω>0),经化简后利用“五点法”画其在某一周期内的图象时,列表并填入的部分数据如下表:
(ω>0),经化简后利用“五点法”画其在某一周期内的图象时,列表并填入的部分数据如下表:
x | ① |
|
| ||
f(x) | 0 | 1 | 0 | -1 | 0 |
(1)请直接写出①处应填的值,并求函数f(x)在区间![]() 上的值域;
上的值域;
(2)△ABC的内角A,B,C所对的边分别为a,b,c,已知f(A+![]() )=1,b+c=4,a=
)=1,b+c=4,a=![]() ,求△ABC的面积.
,求△ABC的面积.
