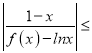Question

【题目】已知函数f(x)＝(2x＋b)ex，F(x)＝bx－ln x，b∈R.

(1)若b<0，且存在区间M，使f(x)和F(x)在区间M上具有相同的单调性，求实数b的取值范围；

(2)若F(x＋1)>b对任意x∈(0，＋∞)恒成立，求实数b的取值范围.

Answer 1

【答案】(1)(－∞，－2).(2)[1，＋∞).

【解析】试题分析：（1）求出函数f（x）的导函数，由导函数的符号求得函数的单调区间，再求出函数F（x）的导函数，由b＜0，可得F′（x）＜0，则F（x）在定义域（0，+∞）上为减函数，要使存在区间M，使f（x）和F（x）在区间M上具有相同的单调性，需＞0，求解可得b的范围；（2）由F（x+1）＞b对任意x∈（0，+∞）恒成立，可得bx﹣ln（x+1）＞0对任意x∈（0，+∞）恒成立，令g（x）=bx﹣ln（x+1），求导可得b≤0时， 0＜b＜1时， b≥1时，这几种情况下的函数最值，求得参数范围。

解析：

(1)f′(x)＝ex(2x＋b＋2)，

由f′(x)<0得x<；由f′(x)>0得.

F(x)的定义域为(0，＋∞)，且F′(x)＝b－，

∵b<0，∴F′(x)<0，即F(x)在(0，＋∞)上单调递减.

∵f(x)和F(x)在区间M上具有相同的单调性，

∴>0，得b<－2，即实数b的取值范围是(－∞，－2).

(2)由F(x＋1)>b得ln(x＋1)－bx<0.

∵x>0， 在x∈(0，＋∞)上恒成立.

设g(x)＝ln(x＋1)－x，则g′(x)＝－1<0，

∴g(x)在(0，＋∞)上递减，∴g(x)<g(0)＝0.

∴ln(x＋1)－x<0，即<1，∴b≥1.

因此实数b的取值范围是[1，＋∞).