题目内容
【题目】已知函数f(x)=![]() (x∈R).
(x∈R).
(1)证明:当a>3时,f(x)在R上是减函数;
(2)若函数f(x)存在两个零点,求a的取值范围.
【答案】(1)见解析;(2)![]()
【解析】
(1)根据题意,由分段函数的解析式依次分析f(x)的两段函数的单调性以及最值,结合函数单调性的定义分析可得答案;
(2)根据题意,函数的解析式变形可得f(x)=3|x-1|-a,分析可得若函数f(x)存在两个零点,即函数f(x)=3|x-1|与函数y=ax有2个不同的交点,结合函数y=3|x-1|的图象分析可得答案.
(1)证明:根据题意,函数f(x)= ![]() ,
,
若a>3,则当x≥1时,f(x)=(3-a)x-3,有(3-a)<0,
此时f(x)为减函数,且f(x)≤f(1)=-a,
当x<1时,f(x)=-(3+a)x+3,有-(3+a)<0,
此时f(x)为减函数,且f(x)>f(1)=-a,
故当a>3时,f(x)为减函数;
(2)根据题意,f(x)= ![]() =3|x-1|-a,
=3|x-1|-a,
若函数f(x)存在两个零点,
即函数f(x)=3|x-1|与函数y=ax有2个不同的交点,

则有0<a<3,
即a的取值范围为(0,3)

【题目】某地区![]() 年至
年至![]() 年农村居民家庭纯收入
年农村居民家庭纯收入![]() (单位:千元)的数据如下表:
(单位:千元)的数据如下表:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入 | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(Ⅰ)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(Ⅱ)利用(Ⅰ)中的回归方程,分析![]() 年至
年至![]() 年该地区农村居民家庭人均纯收入的变化情况,并预测该地区
年该地区农村居民家庭人均纯收入的变化情况,并预测该地区![]() 年农村居民家庭人均纯收入.
年农村居民家庭人均纯收入.
![]() 注:
注: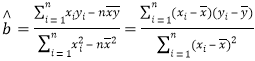 ,
,![]()
![]()
【题目】某种设备随着使用年限的增加,每年的维护费相应增加![]() 现对一批该设备进行调查,得到这批设备自购入使用之日起,前五年平均每台设备每年的维护费用大致如表:
现对一批该设备进行调查,得到这批设备自购入使用之日起,前五年平均每台设备每年的维护费用大致如表:
年份 | 1 | 2 | 3 | 4 | 5 |
维护费 |
|
|
|
|
|
![]() Ⅰ
Ⅰ![]() 求y关于t的线性回归方程;
求y关于t的线性回归方程;
![]() Ⅱ
Ⅱ![]() 若该设备的价格是每台5万元,甲认为应该使用满五年换一次设备,而乙则认为应该使用满十年换一次设备,你认为甲和乙谁更有道理?并说明理由.
若该设备的价格是每台5万元,甲认为应该使用满五年换一次设备,而乙则认为应该使用满十年换一次设备,你认为甲和乙谁更有道理?并说明理由.
![]() 参考公式:
参考公式: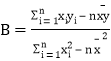 ,
,![]()
【题目】某日A, B, C三个城市18个销售点的小麦价格如下表:
销售点序号 | 所属城市 | 小麦价格(元/吨) | 销售点序号 | 所属城市 | 小麦价格(元/吨) |
1 | A | 2420 | 10 | B | 2500 |
2 | C | 2580 | 11 | A | 2460 |
3 | C | 2470 | 12 | A | 2460 |
4 | C | 2540 | 13 | A | 2500 |
5 | A | 2430 | 14 | B | 2500 |
6 | C | 2400 | 15 | B | 2450 |
7 | A | 2440 | 16 | B | 2460 |
8 | B | 2500 | 17 | A | 2460 |
9 | A | 2440 | 18 | A | 2540 |
(Ⅰ)求B市5个销售点小麦价格的中位数;
(Ⅱ)甲从B市的销售点中随机挑选一个购买1吨小麦,乙从C市的销售点中随机挑选一个购买1吨小麦,求甲花费的费用比乙高的概率;
(Ⅲ)如果一个城市的销售点小麦价格方差越大,则称其价格差异性越大.请你对A、B、C三个城市按照小麦价格差异性从大到小进行排序(只写出结果).

