题目内容
【题目】某校高一（1）（2）两个班联合开展“诗词大会进校园，国学经典润心田”古诗词竞赛主题班会活动，主持人从这两个班分别随机选出20名同学进行当场测试，他们的测试成绩按[40，50），[50，60），[60，70），[70，80），[80，90），[90，100）分组，分别用频率分布直方图与茎叶图统计如图（单位：分）：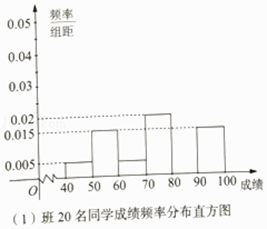 
高一（2）班20名学生成绩茎叶图：
4 | 5 |
5 | 2 |
6 | 4 5 6 8 |
7 | 0 5 5 8 8 8 8 9 |
8 | 0 0 5 5 |
9 | 4 5 |
（Ⅰ）分别计算两个班这20名同学的测试成绩在[80，90）的频率，并补全频率分布直方图；
（Ⅱ）分别从两个班随机选取1人，设这两人中成绩在[80，90）的人数为X，求X的分布列（频率当作概率使用）．
（Ⅲ）运用所学统计知识分析比较两个班学生的古诗词水平．
【答案】解：（I）（1）班的同学成绩在[80，90）的频率为：1﹣（0.005+0.015+0.005+0.02+0.015）×10=0.4， 高一（2）班的同学成绩在[80，90）的频率为： 
=0.2．
补全频率分布直方图如下：
（II）（1）班成绩在[80，90）上的人数有20×0.4=8人，（2）班成绩在[80，90）上的人数有4人，
∴X的可能取值为0，1，2．
P（X=0）= 
= 
，
P（X=1）= 
= 
，
P（X=2）= 
= 
．
∴X的分布列为：
X | 0 | 1 | 2 |
P |
|
|
|
（III）由频率分布直方图看，（1）班的主要成绩集中在[70，100）上，
从茎叶图看，（2）班的主要成绩集中在（60，80）上，
故（1）班的古诗词水平好于（2）班的古诗词水平
【解析】（I）根据面积之和等于1计算（1）班成绩在[80，90）的频率；直角根据公式计算（2）班成绩在[80，90）的频率；（II）利用组合数公式计算概率；（III）根据数据的集中程度得出结论．
【考点精析】本题主要考查了频率分布直方图和离散型随机变量及其分布列的相关知识点，需要掌握频率分布表和频率分布直方图，是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式，可展示数据的分布情况.通过作图既可以从数据中提取信息，又可以利用图形传递信息；在射击、产品检验等例子中，对于随机变量X可能取的值，我们可以按一定次序一一列出，这样的随机变量叫做离散型随机变量．离散型随机变量的分布列：一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn，X取每一个值 xi(i=1,2,......）的概率P(ξ=xi）＝Pi，则称表为离散型随机变量X 的概率分布，简称分布列才能正确解答此题．
