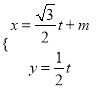МвДїДЪИЭ
ЎѕМвДїЎїДі№«ЛѕјЖ»®№єВт2МЁ»ъЖчЈ¬ёГЦЦ»ъЖчК№УГИэДкєујґ±»МФМ.»ъЖчУРТ»ТЧЛрБгјюЈ¬ФЪ№єЅш»ъЖчК±Ј¬їЙТФ¶оНв№єВтХвЦЦБгјюЧчОЄ±ёјюЈ¬Гїёц200ФЄ.ФЪ»ъЖчК№УГЖЪјдЈ¬Из№ы±ёјюІ»ЧгФЩ№єВтЈ¬ФтГїёц500ФЄ.ПЦРиѕцІЯФЪ№єВт»ъЖчК±У¦Н¬К±№єВтјёёцТЧЛрБгјюЈ¬ОЄґЛЛСјЇІўХыАнБЛ100МЁХвЦЦ»ъЖчФЪИэДкК№УГЖЪДЪёь»»µДТЧЛрБгјюКэЈ¬µГПВГжЦщЧґНјЈє

ТФХв100МЁ»ъЖчёь»»µДТЧЛрБгјюКэµДЖµВКґъМж1МЁ»ъЖчёь»»µДТЧЛрБгјюКэ·ўЙъµДёЕВКЈ¬јЗ![]() ±нКѕ2МЁ»ъЖчИэДкДЪ№ІРиёь»»µДТЧЛрБгјюКэЈ¬
±нКѕ2МЁ»ъЖчИэДкДЪ№ІРиёь»»µДТЧЛрБгјюКэЈ¬![]() ±нКѕ№єВт2МЁ»ъЖчµДН¬К±№єВтµДТЧЛрБгјюКэ.
±нКѕ№єВт2МЁ»ъЖчµДН¬К±№єВтµДТЧЛрБгјюКэ.
ЈЁўсЈ©Зу![]() µД·ЦІјБРЈ»
µД·ЦІјБРЈ»
ЈЁўтЈ©ИфТЄЗу![]() Ј¬И·¶Ё
Ј¬И·¶Ё![]() µДЧоРЎЦµЈ»
µДЧоРЎЦµЈ»
ЈЁўуЈ©ТФ№єВтТЧЛрБгјюЛщРи·СУГµДЖЪНыЦµОЄѕцІЯТАѕЭЈ¬ФЪ![]() Ул
Ул![]() Ц®ЦРСЎЖдТ»Ј¬У¦СЎУГДДёцЈї
Ц®ЦРСЎЖдТ»Ј¬У¦СЎУГДДёцЈї
Ўѕґр°ёЎїЈЁўсЈ©јыЅвОцЈЁўтЈ©19ЈЁўуЈ©![]()
ЎѕЅвОцЎїКФМв·ЦОцЈєЈЁўсЈ©УЙТСЦЄµГXµДїЙДЬИЎЦµОЄ16Ј¬17Ј¬18Ј¬19Ј¬20Ј¬21Ј¬22Ј¬·Ц±рЗуіцПаУ¦µДёЕВКЈ¬УЙґЛДЬЗуіцXµД·ЦІјБРЈ®ЈЁўтЈ©УЙXµД·ЦІјБРЗуіцPЈЁXЎЬ18Ј©=![]() Ј¬PЈЁXЎЬ19Ј©=
Ј¬PЈЁXЎЬ19Ј©=![]() Ј®УЙґЛДЬИ·¶ЁВъЧгPЈЁXЎЬnЈ©ЎЭ0Ј®5ЦРnµДЧоРЎЦµЈ®ЈЁўуЈ©УЙXµД·ЦІјБРµГPЈЁXЎЬ19Ј©=
Ј®УЙґЛДЬИ·¶ЁВъЧгPЈЁXЎЬnЈ©ЎЭ0Ј®5ЦРnµДЧоРЎЦµЈ®ЈЁўуЈ©УЙXµД·ЦІјБРµГPЈЁXЎЬ19Ј©=![]() Ј®ЗуіцВт19ёцЛщРи·СУГЖЪНыEX1єНВт20ёцЛщРи·СУГЖЪНыEX2Ј¬УЙґЛДЬЗуіцВт19ёцёьєПКК
Ј®ЗуіцВт19ёцЛщРи·СУГЖЪНыEX1єНВт20ёцЛщРи·СУГЖЪНыEX2Ј¬УЙґЛДЬЗуіцВт19ёцёьєПКК
КФМвЅвОцЈєЈЁўсЈ©УЙЦщЧґНјІўТФЖµВКґъМжёЕВКїЙµГЈ¬Т»МЁ»ъЖчФЪИэДкДЪРиёь»»µДТЧЛрБгјюКэОЄ8Ј¬9Ј¬10Ј¬11µДёЕВК·Ц±рОЄ0Ј®2Ј¬0Ј®4Ј¬0Ј®2Ј¬0Ј®2Ј¬ґУ¶ш
![]() Ј»
Ј»
![]() Ј»
Ј»
![]() Ј»
Ј»
![]() Ј»
Ј»
![]() Ј»
Ј»
![]() Ј»
Ј»
![]() Ј®
Ј®
ЛщТФ![]() µД·ЦІјБРОЄ
µД·ЦІјБРОЄ
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
|
|
|
|
|
|
|
|
ЈЁўтЈ©УЙЈЁўсЈ©ЦЄ![]() Ј¬
Ј¬![]() Ј¬№К
Ј¬№К![]() µДЧоРЎЦµОЄ19Ј®
µДЧоРЎЦµОЄ19Ј®
ЈЁўуЈ©јЗ![]() ±нКѕ2МЁ»ъЖчФЪ№єВтТЧЛрБгјюЙПЛщРиµД·СУГЈЁµҐО»ЈєФЄЈ©Ј®
±нКѕ2МЁ»ъЖчФЪ№єВтТЧЛрБгјюЙПЛщРиµД·СУГЈЁµҐО»ЈєФЄЈ©Ј®
µ±![]() К±Ј¬
К±Ј¬![]()
![]() Ј®
Ј®
µ±![]() К±Ј¬
К±Ј¬
![]()
![]() Ј®
Ј®
їЙЦЄµ±![]() К±ЛщРи·СУГµДЖЪНыЦµРЎУЪ
К±ЛщРи·СУГµДЖЪНыЦµРЎУЪ![]() К±ЛщРи·СУГµДЖЪНыЦµЈ¬№КУ¦СЎ
К±ЛщРи·СУГµДЖЪНыЦµЈ¬№КУ¦СЎ![]() Ј®
Ј®

 РЗј¶їЪЛгМмМмБ·ПµБРґр°ё
РЗј¶їЪЛгМмМмБ·ПµБРґр°ё Гў№ыЅМёЁґп±кІвКФѕнПµБРґр°ё
Гў№ыЅМёЁґп±кІвКФѕнПµБРґр°ёЎѕМвДїЎїДіРЈёЯТ»ЈЁ1Ј©ЈЁ2Ј©БЅёц°аБЄєПїЄХ№Ў°К«ґКґу»бЅшРЈФ°Ј¬№ъС§ѕµдИуРДМпЎ±№ЕК«ґКѕєИьЦчМв°а»б»о¶ЇЈ¬ЦчіЦИЛґУХвБЅёц°а·Ц±рЛж»ъСЎіц20ГыН¬С§ЅшРРµ±іЎІвКФЈ¬ЛыГЗµДІвКФіЙјЁ°ґ[40Ј¬50Ј©Ј¬[50Ј¬60Ј©Ј¬[60Ј¬70Ј©Ј¬[70Ј¬80Ј©Ј¬[80Ј¬90Ј©Ј¬[90Ј¬100Ј©·ЦЧйЈ¬·Ц±рУГЖµВК·ЦІјЦ±·ЅНјУ뾥ҶͼͳјЖИзНјЈЁµҐО»Јє·ЦЈ©Јє 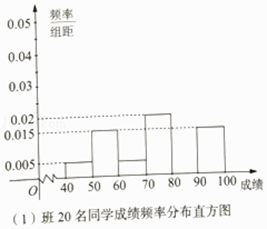
ёЯТ»ЈЁ2Ј©°а20ГыС§ЙъіЙјЁѕҐТ¶НјЈє
4 | 5 |
5 | 2 |
6 | 4 5 6 8 |
7 | 0 5 5 8 8 8 8 9 |
8 | 0 0 5 5 |
9 | 4 5 |
ЈЁўсЈ©·Ц±рјЖЛгБЅёц°аХв20ГыН¬С§µДІвКФіЙјЁФЪ[80Ј¬90Ј©µДЖµВКЈ¬ІўІ№И«ЖµВК·ЦІјЦ±·ЅНјЈ»
ЈЁўтЈ©·Ц±рґУБЅёц°аЛж»ъСЎИЎ1ИЛЈ¬ЙиХвБЅИЛЦРіЙјЁФЪ[80Ј¬90Ј©µДИЛКэОЄXЈ¬ЗуXµД·ЦІјБРЈЁЖµВКµ±ЧчёЕВКК№УГЈ©Ј®
ЈЁўуЈ©ФЛУГЛщС§НіјЖЦЄК¶·ЦОц±ИЅПБЅёц°аС§ЙъµД№ЕК«ґКЛ®ЖЅЈ®
ЎѕМвДїЎї2016ДкИ붬ТФАґЈ¬ёчµШОнцІМмЖшЖµ·ўЈ¬![]() ЖµЖµ±¬±нЈЁ
ЖµЖµ±¬±нЈЁ![]() КЗЦёЦ±ѕ¶РЎУЪ»тµИУЪ2.5ОўГЧµДїЕБЈОпЈ©Ј¬ёчµШ¶Ф»ъ¶ЇіµёьКЗіцМЁБЛёчАаПЮРРґлК©Ј¬ОЄ·ЦОцСРѕїіµБчБїУл
КЗЦёЦ±ѕ¶РЎУЪ»тµИУЪ2.5ОўГЧµДїЕБЈОпЈ©Ј¬ёчµШ¶Ф»ъ¶ЇіµёьКЗіцМЁБЛёчАаПЮРРґлК©Ј¬ОЄ·ЦОцСРѕїіµБчБїУл![]() µДЕЁ¶ИКЗ·сПа№ШЈ¬ДіКРПЦІЙјЇЦЬТ»µЅЦЬОеДіТ»К±јд¶ОіµБчБїУл
µДЕЁ¶ИКЗ·сПа№ШЈ¬ДіКРПЦІЙјЇЦЬТ»µЅЦЬОеДіТ»К±јд¶ОіµБчБїУл![]() µДКэѕЭИзПВ±нЈє
µДКэѕЭИзПВ±нЈє
К±јд | ЦЬТ» | ЦЬ¶ю | ЦЬИэ | ЦЬЛД | ЦЬОе |
іµБчБї | 50 | 51 | 54 | 57 | 58 |
| 69 | 70 | 74 | 78 | 79 |
ЈЁ1Ј©ЗлёщѕЭЙПКцКэѕЭЈ¬ФЪПВГжёшіцµДЧш±кПµЦР»іцЙўµгНјЈ»

ЈЁ2Ј©КФЕР¶П![]() Ул
Ул![]() КЗ·сѕЯУРПЯРФ№ШПµЈ¬ИфУРЗлЗуіц
КЗ·сѕЯУРПЯРФ№ШПµЈ¬ИфУРЗлЗуіц![]() №ШУЪ
№ШУЪ![]() µДПЯРФ»Ш№й·ЅіМ
µДПЯРФ»Ш№й·ЅіМ![]() Ј¬ИфГ»УРЈ¬ЗлЛµГчАнУЙЈ»
Ј¬ИфГ»УРЈ¬ЗлЛµГчАнУЙЈ»
ЈЁ3Ј©ИфЦЬБщН¬Т»К±јд¶ОµДіµБчБїОЄ60НтБѕЈ¬КФёщѕЭЈЁ2Ј©µГіцµДЅбВЫЈ¬Ф¤±ЁёГК±јд¶ОµД![]() µДЕЁ¶ИЈЁ±ЈБфХыКэЈ©.
µДЕЁ¶ИЈЁ±ЈБфХыКэЈ©.
ІОїј№«КЅЈє
 Ј¬
Ј¬![]() .
.
ЎѕМвДїЎїДіЖуТµУРБЅёц·Ці§ЙъІъДіЦЦБгјюЈ¬°ґ№ж¶ЁДЪѕ¶іЯґзЈЁµҐО»ЈєmmЈ©µДЦµВдФЪ[29.94Ј¬30.06Ј©µДБгјюОЄУЕЦКЖ·.ґУБЅёц·Ці§ЙъІъµДБгјюЦРёчійіцБЛ500јюЈ¬БїЖдДЪѕ¶іЯґзЈ¬µГЅб№ыИзПВ±нЈє
јЧі§Јє
·ЦЧй | [29.86Ј¬29.90Ј© | [29.90Ј¬29.94Ј© | [29.94Ј¬29.98Ј© | [29.98Ј¬30.02Ј© | [30.02Ј¬30.06Ј© | [30.06Ј¬30.10Ј© | [30.10Ј¬30.14Ј© |
ЖµКэ | 12 | 63 | 86 | 182 | 92 | 61 | 4 |
ТТі§Јє
·ЦЧй | [29.86Ј¬29.90Ј© | [29.90Ј¬29.94Ј© | [29.94Ј¬29.98Ј© | [29.98Ј¬30.02Ј© | [30.02Ј¬30.06Ј© | [30.06Ј¬30.10Ј© | [30.10Ј¬30.14Ј© |
ЖµКэ | 29 | 71 | 85 | 159 | 76 | 62 | 18 |
ЈЁ1Ј©КФ·Ц±р№АјЖБЅёц·Ці§ЙъІъµДБгјюµДУЕЦКЖ·ВКЈ»
ЈЁ2Ј©УЙТФЙПНіјЖКэѕЭМоПВГж![]() БРБЄ±нЈ¬ІўОККЗ·сУР
БРБЄ±нЈ¬ІўОККЗ·сУР![]() µД°СОХИПОЄЎ°БЅёц·Ці§ЙъІъµДБгјюµДЦКБїУРІоТмЎ±.
µД°СОХИПОЄЎ°БЅёц·Ці§ЙъІъµДБгјюµДЦКБїУРІоТмЎ±.
јЧ і§ | ТТ і§ | єПјЖ | |
УЕЦКЖ· | |||
·ЗУЕЦКЖ· | |||
єПјЖ |
ёЅЈє 
|
|
|
|
|
|
|
|
|
|