题目内容
【题目】在直角坐标系中xOy，直线C1的参数方程为 
（t是参数）．在以坐标原点为极点，x轴非负半轴为极轴的极坐标系中，曲线C2的极坐标方程为ρ=sinθ﹣cosθ（θ是参数）．
（Ⅰ）将曲线C2的极坐标方程化为直角坐标方程，并判断曲线C2所表示的曲线；
（Ⅱ）若M为曲线C2上的一个动点，求点M到直线C1的距离的最大值和最小值．
【答案】解：（I）曲线C2的极坐标方程为ρ=sinθ﹣cosθ（θ是参数）．可得ρ2=ρ（sinθ﹣cosθ），化为直角坐标方程：x2+y2=y﹣x． 配方为： 
= 
．可得曲线C2所表示的曲线为圆：圆心为C2
，半径r= 
．
（Ⅱ）直线C1的参数方程为 
（t是参数），消去参数t化为普通方程：2x﹣y﹣1=0．
圆心C2到直线C1的距离d= 
= 
．
∴点M到直线C1的距离的最大值为 + ，最小值为 ﹣
【解析】（I）曲线C2的极坐标方程为ρ=sinθ﹣cosθ（θ是参数）．可得ρ2=ρ（sinθ﹣cosθ），利用互化公式可得直角坐标方程：通过配方可得曲线C2所表示的曲线为圆．（Ⅱ）直线C1的参数方程为 
（t是参数）．消去参数t化为普通方程：2x﹣y﹣1=0．求出圆心C2到直线C1的距离d．可得点M到直线C1的距离的最大值为d+r，最小值为d﹣r．
名校课堂系列答案
【题目】为调查某地区老年人是否需要志愿者提供帮助，用简单随机抽样方法从该地区调查了500位老年人，结果如下：
男 | 女 | |
需要 | 40 | 30 |
不需要 | 160 | 270 |
（1）估计该地区老年人中，需要志愿者提供帮助的老年人的比例。
（2）能否在犯错误的概率不超过百分之一的前提下认为该地区的老年人是否需要志愿者提供帮助与性别有关？
附：
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【题目】某校高一（1）（2）两个班联合开展“诗词大会进校园，国学经典润心田”古诗词竞赛主题班会活动，主持人从这两个班分别随机选出20名同学进行当场测试，他们的测试成绩按[40，50），[50，60），[60，70），[70，80），[80，90），[90，100）分组，分别用频率分布直方图与茎叶图统计如图（单位：分）：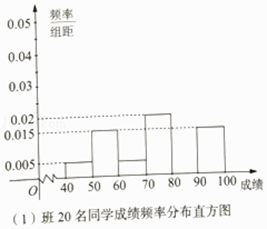 
高一（2）班20名学生成绩茎叶图：
4 | 5 |
5 | 2 |
6 | 4 5 6 8 |
7 | 0 5 5 8 8 8 8 9 |
8 | 0 0 5 5 |
9 | 4 5 |
（Ⅰ）分别计算两个班这20名同学的测试成绩在[80，90）的频率，并补全频率分布直方图；
（Ⅱ）分别从两个班随机选取1人，设这两人中成绩在[80，90）的人数为X，求X的分布列（频率当作概率使用）．
（Ⅲ）运用所学统计知识分析比较两个班学生的古诗词水平．
