题目内容
【题目】(1)
为何值时，
.①有且仅有一个零点；②有两个零点且均比－1大；
(2)若函数
有4个零点，求实数
的取值范围．
【答案】(1) ① m＝4或m＝－1；②(－5，－1)；(2) (－4,0)．
【解析】
试题（1）①
有且仅有一个零点方程
有两个相等实根Δ＝0；②设f(x)的两个零点分别为
，则
＝－2m，
＝3m＋4.由题意，知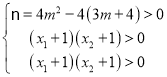
；
（2）数形结合，作出g(x)＝|4x－x2|和h(x)＝－a的图象即可.
试题解析：
(1)①有且仅有一个零点方程有两个相等实根Δ＝0，即4m2－4(3m＋4)＝0，即m2－3m－4＝0，∴m＝4或m＝－1.
②设f(x)的两个零点分别为，
则＝－2m，＝3m＋4.
由题意，知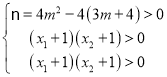
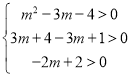
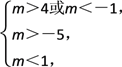
∴－5＜m＜－1.故m的取值范围为(－5，－1)．
(2)令f(x)＝0，得|4x－x2|＋a＝0，
则|4x－x2|＝－a.
令g(x)＝|4x－x2|，
h(x)＝－a.
作出g(x)，h(x)的图象．
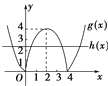
由图象可知，当0＜－a＜4，
即
时，g(x)与h(x)的图象有4个交点.
练习册系列答案
相关题目
