题目内容
(本小题满分12分)
已知等差数列{an}中a2=8,S10=185.
(1)求数列{an}的通项公式an;
(2)若从数列{an}中依次取出第2,4,8,…,2n,…项,按原来的顺 序排成一个新数列{bn},试求{bn}的前n项和An.
序排成一个新数列{bn},试求{bn}的前n项和An.
已知等差数列{an}中a2=8,S10=185.
(1)求数列{an}的通项公式an;
(2)若从数列{an}中依次取出第2,4,8,…,2n,…项,按原来的顺
 序排成一个新数列{bn},试求{bn}的前n项和An.
序排成一个新数列{bn},试求{bn}的前n项和An.
解:(1)设{an}的首项为a,公差为d,
∴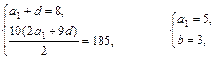 ∴an=5+3(n-1),即an=3n+2
∴an=5+3(n-1),即an=3n+2
(2)设b1=a2,b2=a4,b3=a8,bn=a2n=3×2n+2
∴An=(3×2+2) +(3×22+2)+…+(3×2n+2)=3×(2+22+…+2n)+2n
+(3×22+2)+…+(3×2n+2)=3×(2+22+…+2n)+2n
=3×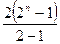 +2n=6×2n-6+2n
+2n=6×2n-6+2n
∴
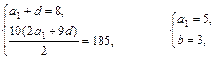 ∴an=5+3(n-1),即an=3n+2
∴an=5+3(n-1),即an=3n+2(2)设b1=a2,b2=a4,b3=a8,bn=a2n=3×2n+2
∴An=(3×2+2)
 +(3×22+2)+…+(3×2n+2)=3×(2+22+…+2n)+2n
+(3×22+2)+…+(3×2n+2)=3×(2+22+…+2n)+2n=3×
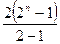 +2n=6×2n-6+2n
+2n=6×2n-6+2n略

练习册系列答案
相关题目
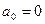 ,
,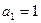 ,点
,点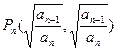 在圆
在圆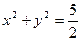 上,
上,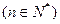
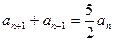 ;
;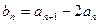
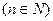 ,求证:数列
,求证:数列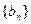 是等比数列;
是等比数列;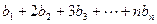
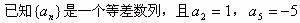

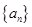 是等差数列且
是等差数列且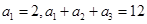 。(1)求数列
。(1)求数列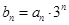 ,求数列
,求数列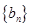 的前
的前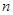 项和
项和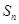 。
。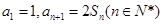 。(1)求数列
。(1)求数列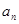 (2)求数列
(2)求数列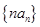 前
前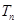 。
。  中,已知
中,已知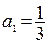 ,
,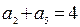 ,
,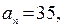 则
则 ( )
( )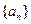 的前
的前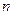 项和为
项和为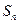 ,若
,若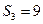 ,
,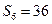 ,则
,则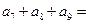
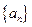 满足
满足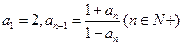 ,则
,则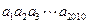 的值的( )
的值的( )
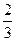
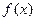 的定义域为
的定义域为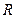 ,且是以2为周期的周期函数,数列
,且是以2为周期的周期函数,数列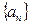 是首项为1,公差为1的等差数列,则
是首项为1,公差为1的等差数列,则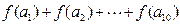 的值为 ( )
的值为 ( ) (
(