题目内容
6.已知圆C:(x-3)2+(y-5)2=5,过圆心C作直线l交圆于A、B两点,交y轴于点P,且2$\overrightarrow{PA}$=$\overrightarrow{PB}$,则直线l的方程为2x-y-1=0或2x+y-11=0.分析 由已知中过圆心C作直线l交圆于A、B两点,交y轴于点P,且2$\overrightarrow{PA}$=$\overrightarrow{PB}$,可得|$\overrightarrow{PA}$|=|$\overrightarrow{AB}$|,即|$\overrightarrow{PC}$|=3|$\overrightarrow{BC}$|=3$\sqrt{5}$,求出P点坐标,代入两点式,可得答案.
解答 解:∵过圆心C作直线l交圆于A、B两点,交y轴于点P,且2$\overrightarrow{PA}$=$\overrightarrow{PB}$,
∴|$\overrightarrow{PA}$|=|$\overrightarrow{AB}$|,即|$\overrightarrow{PC}$|=3|$\overrightarrow{BC}$|=3$\sqrt{5}$,
设P点坐标为(0,b),
则$\sqrt{{3}^{2}+(5-{b)}^{2}}$=3$\sqrt{5}$,
解得:b=11,或b=-1,
故直线l的方程为:$\frac{x}{3}=\frac{y+1}{5+1}$或$\frac{x}{3}=\frac{y-11}{5-11}$,
即2x-y-1=0或2x+y-11=0,
故答案为:2x-y-1=0或2x+y-11=0
点评 本题主要考查直线和圆的位置关系,两点间距离公式,直线的方程,难度不大,属于基础题.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
14.设集合A={x|x2-6x+8<0},B={x|2<2x<8},则A∪B=( )
| A. | {x|2<x<3} | B. | {x|1<x<3} | C. | {x|1<x<4} | D. | {x|3<x<4} |
11.已知等差数列{an}的前三项为a-1,4,2a,记前n项和为Sn,设bn=$\frac{{S}_{n}}{n}$,则b3+b7+b11+…+b4n-1等于( )
| A. | n2+n | B. | 2n2+2n | C. | n2-n | D. | 2n2-2n |
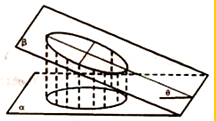 如图,一个底面半径为$\sqrt{3}$的圆柱被与其底面所成角为30°的平面所截,其截面是一个椭圆Γ,以该椭圆Γ的中心为原点,长轴所在的直线
如图,一个底面半径为$\sqrt{3}$的圆柱被与其底面所成角为30°的平面所截,其截面是一个椭圆Γ,以该椭圆Γ的中心为原点,长轴所在的直线 如图,在矩形ABCD中,AB=2BC,E为线段AB的中点,将△ADE沿直线DE翻折成△A′DE,使平面A′DE⊥平面BCD,F为线段A′C的中点.
如图,在矩形ABCD中,AB=2BC,E为线段AB的中点,将△ADE沿直线DE翻折成△A′DE,使平面A′DE⊥平面BCD,F为线段A′C的中点.