题目内容
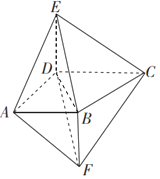
【题目】如图,四棱锥E﹣ABCD的侧棱DE与四棱锥F﹣ABCD的侧棱BF都与底面ABCD垂直,AD⊥CD,AB∥CD,AB=3,AD=4,AE=5,![]() .
.
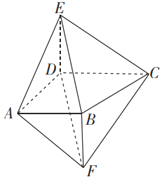
(1)证明:DF∥平面BCE.
(2)求A到平面BEDF的距离,并求四棱锥A﹣BEDF的体积.
【答案】(1)见解析(2)12
【解析】
(1)由DE⊥平面ABCD推出DE⊥AD,勾股定理求出DE,同理由BF⊥平面ABCD求出BF,利用线面垂直的性质推出DE∥BF,结合![]() 推出
推出![]() ,即可证明线面平行;(2)等体积法列出
,即可证明线面平行;(2)等体积法列出![]() ,即可求得A到平面BEDF的距离,四棱锥A﹣BEDF的体积V
,即可求得A到平面BEDF的距离,四棱锥A﹣BEDF的体积V![]() ,代入相应值求解即可.
,代入相应值求解即可.
(1)证明:∵DE⊥平面ABCD,∴DE⊥AD,
∵AD=4,AE=5,∴DE![]() 3,
3,
∵BF⊥平面ABCD,∴BF⊥AB,
∵AB=3,AF![]() ,可得BF
,可得BF![]() 3,
3,
又DE⊥平面ABCD,BF⊥平面ABCD,∴DE∥BF,
又BF=DE,∴四边形BEDF为平行四边形,故DF∥BE,
∵BE平面BCE,DF![]() 平面BCE,
平面BCE,
∴DF∥平面BCE;
(2)设A到平面BEDF的距离为h,
由已知可得,△DAB是以∠DAB为直角的直角三角形,且AB=3,AD=4,
则BD=5,又DE⊥平面ABCD,且DE=3,
由VE﹣ADB=VA﹣BDE,得![]() ,
,
得h![]() ,即A到平面BEDF的距离为
,即A到平面BEDF的距离为![]() ;
;
四棱锥A﹣BEDF的体积V![]() 12.
12.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目