题目内容
【题目】如图,四棱锥![]() 的底面为直角梯形,
的底面为直角梯形,![]()
![]() ,平面
,平面![]() 底面
底面![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 为正三角形,
为正三角形,![]() 是棱
是棱![]() 上的一点(异于端点).
上的一点(异于端点).
(Ⅰ)若![]() 为
为![]() 中点,求证:
中点,求证:![]() 平面
平面![]() ;
;
(Ⅱ)是否存在点![]() ,使二面角
,使二面角![]() 的大小为30°.若存在,求出点
的大小为30°.若存在,求出点![]() 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
【答案】(I)证明见解析;(II)![]() 为棱
为棱![]() 上靠近端点
上靠近端点![]() 的四等分点,证明见解析.
的四等分点,证明见解析.
【解析】
试题分析:(Ⅰ)由已知条件可得四边形![]() 为平行四边形,进而
为平行四边形,进而![]() ,即得
,即得![]() 平面
平面![]() ;(Ⅱ)建立如图所示空间直角坐标系,利用向量法求出
;(Ⅱ)建立如图所示空间直角坐标系,利用向量法求出 ,进而得到存在点
,进而得到存在点![]() 满足,且
满足,且![]() 为棱
为棱![]() 上靠近端点
上靠近端点![]() 的四等分点.
的四等分点.
试题解析:(Ⅰ)证明:如图,连接![]() 交
交![]() 与点
与点![]() ,连接
,连接![]()
由题意知![]() 且
且![]() ,故四边形
,故四边形![]() 为平行四边形
为平行四边形
∴![]() 为
为![]() 中点
中点
∴在![]() 中,又由
中,又由![]() 为
为![]() 中点有:
中点有:![]()
又![]() 面
面![]() ,
,![]() 面
面![]()
∴![]() 平面
平面![]() .
.
(Ⅱ)连接![]() ,则由题意易知
,则由题意易知![]() 平面
平面![]()
故以![]() 为坐标原点建立如图所示空间直角坐标系,则
为坐标原点建立如图所示空间直角坐标系,则
![]()
设![]() ,则
,则![]()
∴![]()
记平面![]() 的法向量
的法向量![]() ,平面
,平面![]() 的法向量
的法向量![]() ,
,
则由 有
有
令![]() 可得
可得![]()
又由 有
有![]() ,即
,即
故存在点![]() 满足,且
满足,且![]() 为棱
为棱![]() 上靠近端点
上靠近端点![]() 的四等分点.
的四等分点.
(其它方法酌情给分).


【题目】某中学一位高三班主任对本班50名学生学习积极性和对待班级工作的态度进行调查,得到的统计数据如下表所示:
积极参加班级工作 | 不积极参加班级工作 | 合计 | |
学习积极性高 | 18 | 7 | 25 |
学习积极性不高 | 6 | 19 | 25 |
合计 | 24 | 26 | 50 |
(1)如果随机调查这个班的一名学生,那么抽到不积极参加班级工作且学习积极性不高的学生的概率是多少?
(2)若不积极参加班级工作且学习积极性高的7名学生中有两名男生,现从中抽取两名学生参加某项活动,问两名学生中有1名男生的概率是多少?
(3)学生的学习积极性与对待班极工作的态度是否有关系?请说明理由.
附:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
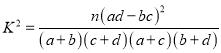
【题目】某单位需要从甲、乙![]() 人中选拔一人参加新岗位培训,特别组织了
人中选拔一人参加新岗位培训,特别组织了![]() 个专项的考试,成绩统计如下:
个专项的考试,成绩统计如下:
第一项 | 第二项 | 第三项 | 第四项 | 第五项 | |
甲的成绩 |
|
|
|
|
|
乙的成绩 |
|
|
|
|
|
(1)根据有关统计知识,回答问题:若从甲、乙![]() 人中选出
人中选出![]() 人参加新岗培训,你认为选谁合适,请说明理由;
人参加新岗培训,你认为选谁合适,请说明理由;
(2)根据有关槪率知识,解答以下问题:
从甲、乙![]() 人的成绩中各随机抽取一个,设抽到甲的成绩为
人的成绩中各随机抽取一个,设抽到甲的成绩为![]() ,抽到乙的成绩为
,抽到乙的成绩为![]() ,用
,用![]() 表示满足条件
表示满足条件![]() 的事件,求事件
的事件,求事件![]() 的概率.
的概率.