题目内容
6.在△ABC中,角A,B,C所对的边分别为a,b,c,若1+$\frac{tanA}{tanB}$=$\frac{2c}{b}$.(1)求角A的大小;
(2)若函数f(x)=2sin2(x+$\frac{π}{4}$)-$\sqrt{3}$cos2x,x∈[$\frac{π}{4}$,$\frac{π}{2}$],在x=B处取到最大值a,求△ABC的面积.
分析 (1)把已知等式中的切化弦,利用正弦定理把边转化为角的正弦,整理可求得cosA的值,进而求得A.
(2)把利用两角和公式对函数解析式化简,利用正弦函数的性质求得函数最大值时B,C和a的值,进而利用正弦定理求得c,最后利用三角形面积公式求得答案.
解答 解:(1)因为1+$\frac{sinA}{cosA}$•$\frac{cosB}{sinB}$=$\frac{2sinC}{sinB}$,
所以$\frac{sinC}{cosA}$=2sinC,
又因为sinC≠0,所以cosA=$\frac{1}{2}$,
所以A=$\frac{π}{3}$.
(2)因为f(x)=2sin2(x+$\frac{π}{4}$)-$\sqrt{3}$cos2x=1+2sin(2x-$\frac{π}{3}$),
所以,当2x-$\frac{π}{3}$=$\frac{π}{2}$,即x=$\frac{5π}{12}$时,f(x)max=3,
此时B=$\frac{5π}{12}$,C=$\frac{π}{4}$,a=3.
因为$\frac{a}{sinA}$=$\frac{c}{sinC}$,所以c=$\frac{asinC}{sinA}$=$\frac{3×\frac{\sqrt{2}}{2}}{\frac{\sqrt{3}}{2}}$=$\sqrt{6}$,
则S=$\frac{1}{2}$acsinB=$\frac{1}{2}$×3×$\sqrt{6}$×$\frac{\sqrt{6}+\sqrt{2}}{4}$=$\frac{9+3\sqrt{3}}{4}$.
点评 本题主要考查了正弦定理和三角函数图象与性质.考查了学生基础公式的运用和一定的运算能力.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
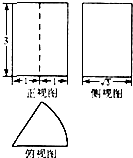
17.已知某几何体的三视图如图所示,其中俯视图是扇形,则该几何体的体积为( )

| A. | 4 π | B. | 2 π | C. | $\frac{4π}{3}$ | D. | $\frac{2π}{3}$ |
1.已知椭圆M:$\frac{{x}^{2}}{4}$+y2=1的上、下顶点为A,B,过点P(0,2)的直线l与椭圆M相交于两个不同的点C,D(C在线段PD之间),则$\overrightarrow{OC}$•$\overrightarrow{OD}$的取值范围( )
| A. | (-1,16) | B. | [-1,16] | C. | (-1,$\frac{13}{4}$) | D. | [-1,$\frac{13}{4}$) |
18.在平行六面体ABCD-A1B1C1D1中,若AA1=AB=AD=1,∠A1AD=∠A1AB=∠BAD=60°,则直线AC1与平面ABCD所成的角的余弦值为( )
| A. | $\frac{{\sqrt{2}}}{3}$ | B. | $\frac{{2\sqrt{2}}}{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{6}}}{3}$ |