题目内容
19.已知平面直角坐标系xOy上的区域D由不等式组$\left\{\begin{array}{l}{y≤2}\\{0≤x≤\sqrt{2}}\\{x-\sqrt{2}y≤0}\end{array}\right.$确定,若M(x,y)为D上的动点,则Z=$\sqrt{2}$x+y的最大值为( )| A. | 4 | B. | 4$\sqrt{2}$ | C. | 3 | D. | 3$\sqrt{2}$ |
分析 画出满足已知不等式组$\left\{\begin{array}{l}{y≤2}\\{0≤x≤\sqrt{2}}\\{x-\sqrt{2}y≤0}\end{array}\right.$确定的可行域,并求出各角点的坐标,代入目标函数中分别求出目标函数的值,比较后可得目标函数的最大值
解答 解:满足不等式组$\left\{\begin{array}{l}{y≤2}\\{0≤x≤\sqrt{2}}\\{x-\sqrt{2}y≤0}\end{array}\right.$确定的可行域如下图中阴影部分所示: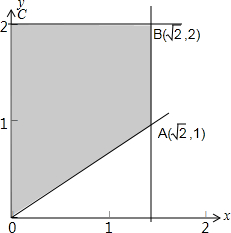 ∵z=$\sqrt{2}$x+y,则y=-$\sqrt{2}$x+z,
∵z=$\sqrt{2}$x+y,则y=-$\sqrt{2}$x+z,
∴zO=0,zA=3,zB=4,zC=2,
故z=的最大值为4;
故选A.
点评 本题考查的知识点是简单的线性规划,熟练掌握角点法是快速准确的解答线性规划题的关键;考查了数形结合的思想.

练习册系列答案
相关题目
9.设α为第二象限角,若tanα=-$\frac{3}{4}$,则cos(α+$\frac{π}{4}$)=( )
| A. | -$\frac{\sqrt{2}}{10}$ | B. | $\frac{\sqrt{2}}{10}$ | C. | -$\frac{7\sqrt{2}}{10}$ | D. | $\frac{7\sqrt{2}}{10}$ |
10.设实数a,b是方程|lgx|=c的两个不同的实根,若a<b<10,则abc的取值范围是( )
| A. | (0,1) | B. | (1,10) | C. | (10,100) | D. | (1,100) |
7.已知I为实数集,M={x|x2-2x<0},N={y|y=$\sqrt{x-1}$},则M∩N=( )
| A. | {x|0<x<1} | B. | {x|0<x<2} | C. | {x|1≤x<2} | D. | ∅ |
14.已知圆C:(x+1)2+(y-2)2=20,直线L:mx-y+1-m=0,直线L被圆C截得的弦长最小时L的方程是( )
| A. | x+y-2=0 | B. | 2x-y-1=0 | C. | 3x-y-2=0 | D. | 4x-2y-3=0 |
4.已知全集U={1,2,3,4,5},A={1,2},B={2,3,4},则(∁UA)∩B=( )
| A. | {2,3} | B. | {3,4} | C. | {3} | D. | {4} |
2.下列命题中,真命题是( )
| A. | 命题?x∈R,2x>x2的否定是真命题 | B. | a>1,b>1是ab>1的充要条件 | ||
| C. | {x|x2-4>0}∩{x|x-1<0}=(-2,1) | D. | ?x0∈R,ex0≤0 |
20.已知曲线y=$\frac{1}{3}{x^3}$经过点$P(2,\frac{8}{3})$,则在P点处的切线方程为( )
| A. | 3x-12y-16=0 | B. | 12x-3y-16=0 | C. | 3x-12y+16=0 | D. | 12x-3y+16=0 |