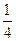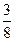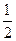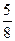题目内容
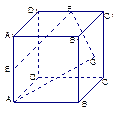
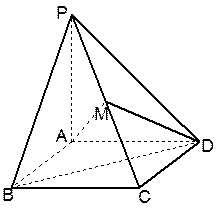
在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PA 底面ABCD,点M是棱PC的中点,AM
底面ABCD,点M是棱PC的中点,AM PBD.
PBD.
(1)求PA的长
(2)证明PB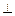 平面AMD
平面AMD
(3)求棱PC与平面AMD所成角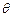 的余弦值.
的余弦值.
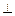 底面ABCD,点M是棱PC的中点,AM
底面ABCD,点M是棱PC的中点,AM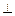 PBD.
PBD.
(1)求PA的长
(2)证明PB
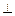 平面AMD
平面AMD (3)求棱PC与平面AMD所成角
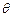 的余弦值.
的余弦值.1,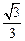
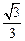
解:(1)首先建好空间直角坐标系,以A为原点,
AB为x轴,AD为y轴,AP为z轴.
设
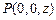 ,由已知得
,由已知得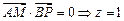 ,
,所以PA的长为1;
(2)先证明
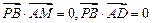 ,
,从而得PB
 平面AMD;
平面AMD;(3)平面AMD的法向量为
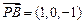 ,
,又
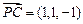 ,
,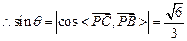 ,
,所以棱PC与平面AMD所成角
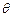 的余弦值为
的余弦值为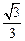 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
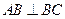 ,
,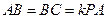 ,点
,点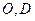 分别是AC、PC的中点,
分别是AC、PC的中点,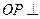 底面AB
底面AB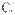
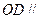 平面
平面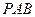 ;
;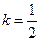 时,求
时,求 直线
直线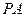 与平面
与平面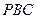 所成的角的大小;
所成的角的大小;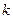 取何值时,
取何值时, 在平面
在平面 的重心?
的重心?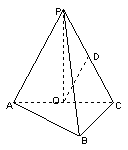
 中,底面
中,底面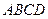 为矩形,
为矩形,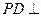 底面
底面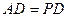 ,
,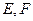 分别为
分别为 的中点
的中点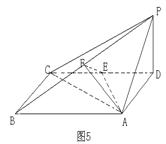
 面
面 ;
; ,求
,求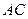 与面
与面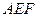 所成角的余弦值
所成角的余弦值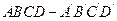 为正方体, 点
为正方体, 点 在
在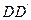 的延长线上,
的延长线上,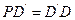 ,
,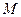 、
、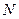 分别为
分别为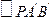 和
和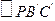 的重心.
的重心. )已知
)已知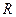 为棱
为棱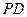 上任意一点,求证:
上任意一点,求证: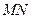 ∥面
∥面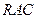 ;
;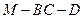 的大
的大 小.
小. 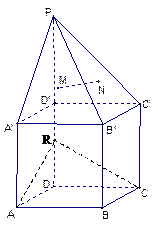
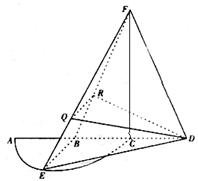
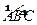 是半径为a的半圆,AC为直径,点E为
是半径为a的半圆,AC为直径,点E为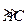 的中点,点B和点C为线段AD的三等分点.平面AEC外一点F满足
的中点,点B和点C为线段AD的三等分点.平面AEC外一点F满足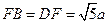 ,FE=
,FE=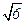 a .
a .
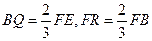 ,求平面
,求平面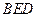 与平面
与平面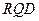 所成二面角的正弦值
所成二面角的正弦值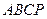 中,
中,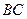 ∥
∥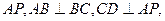
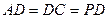 =2,
=2, 、
、 、
、 分别是
分别是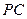 、
、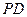 、
、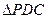 沿
沿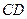 折起,使平面
折起,使平面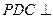 平面
平面 (如图2).
(如图2).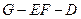 的大小;
的大小; 上确定一点
上确定一点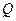 ,使
,使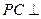 平面
平面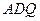 ,并给出证明过程.
,并给出证明过程.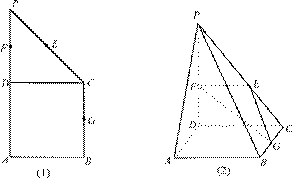
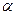 和两条直线a、b,则下列命题中正确的是
和两条直线a、b,则下列命题中正确的是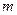 、
、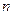 是不同的直线,
是不同的直线,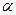 、
、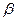 、
、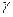 是不同的平面,有以
是不同的平面,有以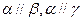 ,则
,则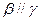 ; ②若
; ②若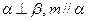 ,则
,则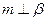 ;
;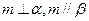 ,则
,则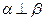 ; ④若
; ④若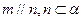 ,则
,则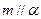 .
.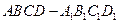 中,
中,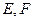 分别为棱
分别为棱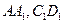 的中点,
的中点,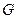 是侧面
是侧面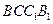 的中心,则空间四边形
的中心,则空间四边形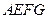 在正方体的六个面上的射影图形面积的最大值是( )
在正方体的六个面上的射影图形面积的最大值是( )