Question

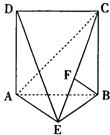
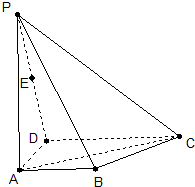
如图，ABCD是梯形，AB∥CD，∠BAD=90°，PA⊥面ABCD，且AB=1，AD=1，CD=2，PA=3，E为PD的中点
（Ⅰ）求证：AE∥面PBC．
（Ⅱ）求直线AC与PB所成角的余弦值；
（Ⅲ）在面PAB内能否找一点N，使NE⊥面PAC．若存在，找出并证明；若不存在，请说明理由．

Answer 1

（Ⅰ）取PC中点为F，连接EF，BF
又E为PD的中点，所以EF∥DC且EF=

1

2

DC
所以EF∥AB，且EF=AB，所以ABFE为平行四边形（2分）
所以AE∥BF，因为AE?面PBC，所以AE∥面PBC（4分）
（Ⅱ）建立如图所示的空间直角坐标系，
则A、B、C、D、P、E的坐标分别为A（0，0，0），
B（1，0，0），C（2，1，0），D（0，1，0），
P（0，0，3），E（0，

1

2

，

3

2

）（5分）
从而

AC

=（2，1，0），

PB

=（1，0，-3）
设

AC

与

PB

的夹角为θ，则
cosθ=

AC • PB

| AC |•| PB |

=-

2

5

，（7分）
∴AC与PB所成角的余弦值为

2

5

（8分）
（Ⅲ）在面ABCD内过D作AC的垂线交AB于G，连PG，
设N为PG的中点，连NE，则NE∥DG，（10分）
∵DG⊥AC，DG⊥PA，∴DG⊥面PAC从而NE⊥面PAC（14分）