题目内容
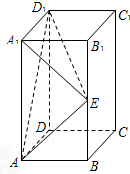
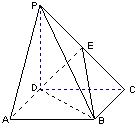
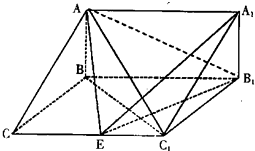
如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,已知BB1=2,AB=
,BC=1,∠BCC1=
(1)求证:C1B⊥平面ABC;
(2)试在棱CC1(不包含端点C,C1)上确定一点E的位置,使得EA⊥EB1.
| 2 |
| π |
| 3 |
(1)求证:C1B⊥平面ABC;
(2)试在棱CC1(不包含端点C,C1)上确定一点E的位置,使得EA⊥EB1.

(I)证明:∵AB⊥侧面BB1C1C,∴AB⊥BC1.
在△BC1C中,BC=1,CC1=BB1=2,∠BCC1=
,
由余弦定理得BC12=BC2+CC12-2BC•CC1COS
=12+22-2×1×2×
=3,∴BC1=
.
故有BC2+BC21=CC21,∴C1B⊥BC,
而BC∩AB=B且AB,BC?平面ABC,
∴C1B⊥平面ABC.
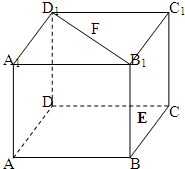
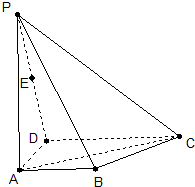
(II)如图所示: 以线段BB1为直径画圆O,分别交线段CC1于点E、C1.
以线段BB1为直径画圆O,分别交线段CC1于点E、C1.
下面说明点E、C1是上述所画的圆与线段CC1的交点.
①∵B1C1=OB1=1,∠OB1C1=
,∴△OB1C1是正三角形,∴OC1=1,即点C1在所画的圆上.
②作OK⊥CC1,垂足为K,取EK=KC1,则点E也在所画的圆上.
∵OE=OC1=1,∴点E也在所画的圆上.
∵CC1∥BB1,∴∠OBE=∠OB1C1=
,∴△OBE是正三角形,∴EB=1,
∴EB=BC=1,又∠BCE=
,∴△BCE为正三角形,∴CE=1,即E点是线段CC1的中点.
下面证明点E满足条件.
∵AB⊥侧面BB1C1C,B1E⊥BE,据三垂线定理可得B1E⊥AE.
故线段CC1的中点E即是要求的点.
在△BC1C中,BC=1,CC1=BB1=2,∠BCC1=
| π |
| 3 |
由余弦定理得BC12=BC2+CC12-2BC•CC1COS
| π |
| 3 |
| 1 |
| 2 |
| 3 |
故有BC2+BC21=CC21,∴C1B⊥BC,
而BC∩AB=B且AB,BC?平面ABC,
∴C1B⊥平面ABC.
(II)如图所示:
 以线段BB1为直径画圆O,分别交线段CC1于点E、C1.
以线段BB1为直径画圆O,分别交线段CC1于点E、C1.下面说明点E、C1是上述所画的圆与线段CC1的交点.
①∵B1C1=OB1=1,∠OB1C1=
| π |
| 3 |
②作OK⊥CC1,垂足为K,取EK=KC1,则点E也在所画的圆上.
∵OE=OC1=1,∴点E也在所画的圆上.
∵CC1∥BB1,∴∠OBE=∠OB1C1=
| π |
| 3 |
∴EB=BC=1,又∠BCE=
| π |
| 3 |
下面证明点E满足条件.
∵AB⊥侧面BB1C1C,B1E⊥BE,据三垂线定理可得B1E⊥AE.
故线段CC1的中点E即是要求的点.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目