题目内容
【题目】已知函数f(x)=ax2+bx+c(a≠0),满足f(0)=2,f(x+1)﹣f(x)=2x﹣1
(1)求函数f(x)的解析式;
(2)当x∈[﹣1,2]时,求函数的最大值和最小值.
(3)若函数g(x)=f(x)﹣mx的两个零点分别在区间(﹣1,2)和(2,4)内,求m的取值范围.
【答案】(1)![]() ;(2)最大值
;(2)最大值![]() ,最小值
,最小值![]() ;(3)
;(3)![]() .
.
【解析】
(1)由f(0)=2,可以求出c 的值,再利用f(x+1)﹣f(x)=2x﹣1可以求出a和b的值,进而求出函数f(x)的解析式;(2)函数f(x)是二次函数,利用二次函数在[﹣1,2]的单调性可以求出最大值和最小值;(3)利用g(x)的两个零点分别在区间(﹣1,2)和(2,4)内,列出不等式组,即可求出m的取值范围。
(1)由f(0)=2,得c=2,
又f(x+1)﹣f(x)=2x﹣1
得2ax+a+b=2x﹣1,故解得:a=1,b=﹣2,
所以f(x)=x2﹣2x+2.
(2)f(x)=x2﹣2x+2=(x﹣1)2+1,对称轴为x=1在[﹣1,2]内,
所以f(x)在[﹣1,1]单调递减,在(1,2]单调递增,
故fmin(x)=f(1)=1,
又f(﹣1)=5,f(2)=2,而5>2
所以fmax(x)=f(﹣1)=5.
(3)![]() =x2﹣(2+m)x+2,若g(x)的两个零点分别在区间(﹣1,2)和(2,4)内,
=x2﹣(2+m)x+2,若g(x)的两个零点分别在区间(﹣1,2)和(2,4)内,
则满足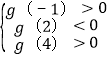 即
即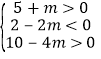
解得:![]() .
.
故答案为![]() .
.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
