题目内容
【题目】已知点![]() 是函数
是函数![]() (
(![]() ),且
),且![]() )的图象上一点,等比数列
)的图象上一点,等比数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]() (
(![]() )的首项为
)的首项为![]() ,且前
,且前![]() 项和
项和![]() 满足:
满足: ![]() (
(![]() ).
).
(1).求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2).若数列![]() 的通项
的通项![]() 求数列
求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3).若数列![]() 前
前![]() 项和为
项和为![]() ,试问
,试问![]() 的最小正整数
的最小正整数![]() 是多少.
是多少.
【答案】( 1)![]()
![]() (2)
(2)![]() (3)112
(3)112
【解析】
(1)先求a,再根据等比中项求c,根据等比数列通项公式求![]() 的通项公式,根据条件得
的通项公式,根据条件得![]() 为等差数列,解得
为等差数列,解得![]() ,再根据和项与通项关系求
,再根据和项与通项关系求![]() 的通项公式;(2)根据错位相减法求数列
的通项公式;(2)根据错位相减法求数列![]() 的前
的前![]() 项和
项和![]() ;(3)根据裂项相消法求数列
;(3)根据裂项相消法求数列![]() 前
前![]() 项和为
项和为![]() ,解不等式得最小正整数
,解不等式得最小正整数![]() .
.
(1).因为![]() 所以
所以![]() ,
,
![]() ,
,![]() ,
,![]() .
.
又数列![]() 成等比数列,
成等比数列, 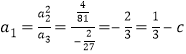 ,所以
,所以![]() .
.
于是公比![]() ,所以
,所以![]()
![]() .
.
因为![]()
![]() ,
,
又![]() ,
,![]() ,所以
,所以![]()
故数列![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列,于是
的等差数列,于是![]() ,所以
,所以![]() .
.
于是当![]() 时,
时, ![]() ; (*)
; (*)
又因为![]() 也满足(*)式,所以
也满足(*)式,所以![]()
![]() .
.
(2).∵![]() ,
,![]() ,
,
∴![]() ,①
,①
![]()
![]() ,②
,②
由①-②得![]()
![]() ,
,
化简得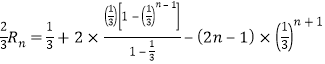
![]() ,
,
∴![]() .
.
(3). 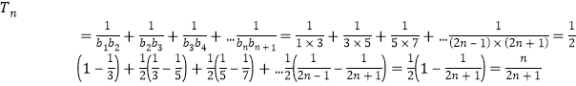
由![]() 得
得![]() ,
,
故满足![]() 的最小正整数为
的最小正整数为![]() .
.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目

