题目内容
双曲线方程为x -2y
-2y =1.则它的右焦点坐标是( )
=1.则它的右焦点坐标是( )
A.( ,0) ,0) | B.( ,0) ,0) | C.( ,0) ,0) | D.( ,0) ,0) |
C
解析试题分析:根据双曲线的方程可知,双曲线方程为x -2y
-2y =1.焦点在x轴上,且
=1.焦点在x轴上,且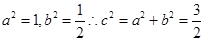 ,那么可知
,那么可知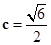 ,因此可知右焦点坐标为(
,因此可知右焦点坐标为( ,0),选C.
,0),选C.
考点:双曲线的基本性质
点评:本题主要考查双曲线的基本性质.在求双曲线的焦点时,一定要先判断出焦点所在位置,在下结论,以免出错.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
若双曲线 (
( ,
, )的一条渐近线被圆
)的一条渐近线被圆 截得的弦长为
截得的弦长为 ,则双曲线的离心率为
,则双曲线的离心率为
A. | B. |
C. | D. |
已知抛物线 的焦点
的焦点 与双曲线
与双曲线 的右焦点重合,抛物线的准线与
的右焦点重合,抛物线的准线与 轴的交点为
轴的交点为 ,点
,点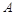 在抛物线上且
在抛物线上且 ,则
,则 的面积为( )
的面积为( )
| A.4 | B.8 | C.16 | D.32 |
已知F1、F2分别是双曲线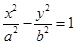 的左、右焦点,P为双曲线右支上的任意一点.若
的左、右焦点,P为双曲线右支上的任意一点.若 ,则双曲线离心率的取值范围是( )
,则双曲线离心率的取值范围是( )
| A.(1,2] | B.[2 + ) ) | C.(1,3] | D.[3,+ ) ) |
已知 是抛物线
是抛物线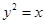 的焦点,
的焦点,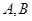 是抛物线上的两点,
是抛物线上的两点, ,则线段
,则线段 的中点
的中点 到
到 轴的距离为( )
轴的距离为( )
A. | B.1 | C. | D. |
若 是任意实数,则方程x2+4y2sin
是任意实数,则方程x2+4y2sin =1所表示的曲线一定不是( )
=1所表示的曲线一定不是( )
| A.圆 | B.双曲线 | C.直线 | D.抛物线 |
 焦点的直线交抛物线于A、B两点,则
焦点的直线交抛物线于A、B两点,则 的最小值为
的最小值为  B.
B.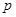 C.
C. D.无法确定
D.无法确定 =4x,O为坐标原点,P为抛物线的准线与其对称轴的交点,过焦点F且垂直于x轴的直线交抛物线于M、N两点,若直线PM与ON相交于点Q,则cos∠MQN=
=4x,O为坐标原点,P为抛物线的准线与其对称轴的交点,过焦点F且垂直于x轴的直线交抛物线于M、N两点,若直线PM与ON相交于点Q,则cos∠MQN=

 为双曲线
为双曲线 的左焦点,在
的左焦点,在 轴上
轴上 ,以
,以 为直径的圆与双曲线左、右两支在
为直径的圆与双曲线左、右两支在 、
、 ,则
,则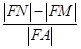 的值为( )
的值为( )


