题目内容
已知抛物线 的焦点
的焦点 与双曲线
与双曲线 的右焦点重合,抛物线的准线与
的右焦点重合,抛物线的准线与 轴的交点为
轴的交点为 ,点
,点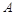 在抛物线上且
在抛物线上且 ,则
,则 的面积为( )
的面积为( )
| A.4 | B.8 | C.16 | D.32 |
D
解析试题分析:解:点A在抛物线准线上的射影为D,根据抛物线性质可知|AF|=|AD|,∵双曲线 的右焦点为(4,0),即抛物线焦点为(4,0)∴
的右焦点为(4,0),即抛物线焦点为(4,0)∴ ∵|AK|=
∵|AK|=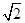 |AF|=
|AF|=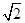 |AD|,∴∠DKA=∠AKF=45°,设A点坐标为(
|AD|,∴∠DKA=∠AKF=45°,设A点坐标为( ,y0),则有
,y0),则有 +4=y0,解得y0=8,∴|AK|=8
+4=y0,解得y0=8,∴|AK|=8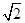 ∴△AFK的面积为
∴△AFK的面积为 •|AK|•|KF|sin45°=32,故选D
•|AK|•|KF|sin45°=32,故选D
考点:抛物线的性质
点评:本题主要考查了抛物线的性质.属基础题

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
过椭圆 的左焦点
的左焦点 作直线
作直线 交椭圆于
交椭圆于 两点,
两点, 是椭圆右焦点,则
是椭圆右焦点,则 的周长为( )
的周长为( )
A. | B. | C. | D. |
已知双曲线的一个焦点为 ,点
,点 位于该双曲线上,线段
位于该双曲线上,线段 的中点坐标为
的中点坐标为 ,则该双曲线的标准方程为
,则该双曲线的标准方程为
A. | B. | C. | D. |
已知实数 构成一个等比数列,则圆锥曲线
构成一个等比数列,则圆锥曲线 的离心率为( )
的离心率为( )
A. | B.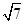 | C. 或 或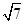 | D. 或7 或7 |
设双曲线 的虚轴长为2,焦距为
的虚轴长为2,焦距为 ,则双曲线的渐近线方程为
,则双曲线的渐近线方程为
A. | B. | C. | D. |
双曲线方程为x -2y
-2y =1.则它的右焦点坐标是( )
=1.则它的右焦点坐标是( )
A.( ,0) ,0) | B.( ,0) ,0) | C.( ,0) ,0) | D.( ,0) ,0) |
已知双曲线 =1(a>0,b>0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是 ( )
=1(a>0,b>0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是 ( )
| A.[1,2] | B.(1,2) | C.[2,+∞) | D.(2,+∞) |
 的左、右焦点分别为
的左、右焦点分别为 、
、 ,若椭圆
,若椭圆 上恰好有6个不同的点
上恰好有6个不同的点 ,使得
,使得 为等腰三角形,则椭圆
为等腰三角形,则椭圆



 的一条渐近线方程是y=
的一条渐近线方程是y= ,它的一个焦点在抛物线
,它的一个焦点在抛物线 的准线上,则双曲线的方程为
的准线上,则双曲线的方程为



