题目内容
设抛物线C的方程为y =4x,O为坐标原点,P为抛物线的准线与其对称轴的交点,过焦点F且垂直于x轴的直线交抛物线于M、N两点,若直线PM与ON相交于点Q,则cos∠MQN=
=4x,O为坐标原点,P为抛物线的准线与其对称轴的交点,过焦点F且垂直于x轴的直线交抛物线于M、N两点,若直线PM与ON相交于点Q,则cos∠MQN=
A. | B.- | C. | D.- |
D
解析试题分析:解:如图,∵物线C的方程为y2=4x,O为坐标原点,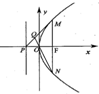
P为抛物线的准线与其对称轴的交点,∴P(-1,0),F(1,0),∵焦点F且垂直于x轴的直线交抛物线于M、N两点,∴M(1,2),N(1,-2),∵直线PM过P(-1,0),M(1,2),∴直线PM的方程为 =1,即y=x+1,∵直线NO过点O(0,0),N(1,-2),∴直线ON的方程是,即y=-2x,解方程组y=x+1与y=-2x,解得
=1,即y=x+1,∵直线NO过点O(0,0),N(1,-2),∴直线ON的方程是,即y=-2x,解方程组y=x+1与y=-2x,解得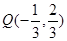 ,那么可知
,那么可知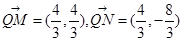 ,结合向量的夹角公式可知cos∠MQN=-
,结合向量的夹角公式可知cos∠MQN=- ,选D.
,选D.
考点:直线与圆锥曲线的综合应用能力
点评:本题主要考查直线与圆锥曲线的综合应用能力,综合性强,难度大,是高考的重点,易错点是抛物线知识体系不牢固.本题具体涉及到轨迹方程的求法及直线与抛物线的相关知识,解题时要注意合理地进行等价转化

练习册系列答案
相关题目
角 的终边经过点A
的终边经过点A ,且点A在抛物线
,且点A在抛物线 的准线上,则
的准线上,则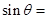 ( )
( )
A. | B. | C. | D. |
已知实数 构成一个等比数列,则圆锥曲线
构成一个等比数列,则圆锥曲线 的离心率为( )
的离心率为( )
A. | B.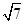 | C. 或 或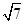 | D. 或7 或7 |
双曲线方程为x -2y
-2y =1.则它的右焦点坐标是( )
=1.则它的右焦点坐标是( )
A.( ,0) ,0) | B.( ,0) ,0) | C.( ,0) ,0) | D.( ,0) ,0) |
如果椭圆 上一点P到焦点F1的距离为6,则点P到另一个焦点F2的距离为( )
上一点P到焦点F1的距离为6,则点P到另一个焦点F2的距离为( )
| A.10 | B.6 | C.12 | D.14 |
已知焦点在 轴上的椭圆
轴上的椭圆 的离心率是
的离心率是 ,则
,则 的值为 ( )
的值为 ( )
A.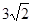 | B. | C. | D. |
 ,曲线C2:
,曲线C2: ,EF是曲线C1的任意一条直径,P是曲线C2上任一点,则
,EF是曲线C1的任意一条直径,P是曲线C2上任一点,则 ·
· 的最小值为 ( )
的最小值为 ( )
 与双曲线
与双曲线 相交于ABCD四点,若四边形ABCD是正方形,则双曲线的离心率的取值范围为( )
相交于ABCD四点,若四边形ABCD是正方形,则双曲线的离心率的取值范围为( )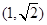



 是双曲线
是双曲线 的左、右焦点,过
的左、右焦点,过 且垂直于
且垂直于 轴的直线与双曲线交于
轴的直线与双曲线交于 两点,若△
两点,若△ 是锐角三角形,则该双曲线离心率的取值范围是( )
是锐角三角形,则该双曲线离心率的取值范围是( )


