Question

【题目】已知向量 ， ， （m＞0，n＞0），若m+n∈[1，2]，则 的取值范围是（ ）
A.
B.
C.
D.

Answer 1

【答案】B
【解析】解：根据题意，向量 ， ， =（3m+n，m﹣3n），
则 = = ，
令t= ，则 = t，
而m+n∈[1，2]，即1≤m+n≤2，在直角坐标系表示如图，
t= 表示区域中任意一点与原点（0，0）的距离，
分析可得： ≤t＜2，
又由 = t，
故 ≤ ＜2 ；
故选：B．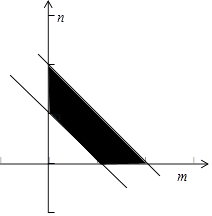

根据题意，由向量的坐标运算公式可得 =（3m+n，m﹣3n），再由向量模的计算公式可得 = ，可以令t= ，将m+n∈[1，2]的关系在直角坐标系表示出来，分析可得t= 表示区域中任意一点与原点（0，0）的距离，进而可得t的取值范围，又由 = t，分析可得答案．