题目内容
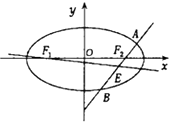
【题目】已知点P是长轴长为 
的椭圆Q： 
上异于顶点的一个动点，O为坐标原点，A为椭圆的右顶点，点M为线段PA的中点，且直线PA与OM的斜率之积恒为 
．
（1）求椭圆Q的方程；
（2）设过左焦点F1且不与坐标轴垂直的直线l交椭圆于C，D两点，线段CD的垂直平分线与x轴交于点G，点G横坐标的取值范围是 
，求|CD|的最小值．
【答案】
（1）解：∵椭圆Q的长轴长为 
，∴ 
．
设P（x0，y0），
∵直线PA与OM的斜率之积恒为 
，∴ 
，
∴ 
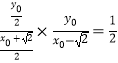，∴b=1，
故椭圆的方程为 
（2）解：设直线l方程为y=k（x+1）（k≠0），代入 有（1+2k2）x2+4k2x+2k2﹣2=0，
设A（x1，y1），B（x2，y2），AB中点N（x0，y0），
∴ 
．
∴ 
∴CD的垂直平分线方程为 
，
令y=0，得 
∵ 
，∴ 
，∴ 
． 
= 
， 
【解析】（1）利用椭圆Q的长轴长为 ，求出 ．设P（x0 ， y0），通过直线PA与OM的斜率之积恒为 ，化简求出b，即可得到椭圆方程．（2）设直线l方程为y=k（x+1）（k≠0），代入 有（1+2k2）x2+4k2x+2k2﹣2=0，设A（x1 ， y1），B（x2 ， y2），AB中点N（x0 ， y0），利用韦达定理求出CD的垂直平分线方程，推出 ，利用弦长公式化简，推出|CD|的最小值．
【考点精析】认真审题，首先需要了解椭圆的标准方程(椭圆标准方程焦点在x轴：
，焦点在y轴：
)．
练习册系列答案
相关题目
