Question

【题目】已知数列满足，且.

（Ⅰ）证明：数列为等差数列，并求数列的通项公式；

（Ⅱ）若记为满足不等式的正整数的个数，设，求数列的最大项与最小项的值.

【答案】(1)见解析;(2)最大项为，最小项为.

【解析】试题分析：（Ⅰ）对两边取倒数，移项即可得出，故而数列为等差数列，利用等差数列的通项公式求出，从而可得出；（Ⅱ）根据不等式，，得，又，从而，当为奇数时，单调递减，；当为偶数时单调递增，综上的最大项为，最小项为.

试题解析：（Ⅰ）由于，，则

∴，则，即为常数

又，∴数列是以1为首项，为公比的等比数列

从而，即.

（Ⅱ）由即，得，

又，从而

故

当为奇数时，，单调递减，；

当为偶数时，，单调递增，

综上的最大项为，最小项为.

【题型】解答题
【结束】
22

【题目】已知向量， ，若函数的最小正周期为，且在区间上单调递减.

（Ⅰ）求的解析式；

（Ⅱ）若关于的方程在有实数解，求的取值范围.

Answer 1

【答案】(1);(2)或.

【解析】试题分析：（Ⅰ）由平面向量数量积公式可得，利用二倍角的正弦公式、二倍角的余弦公式以及两角和与差的正弦公式将函数化为，利用正弦函数的周期公式可得，利用区间上单调递减，可得，从而可得函数解析式；（Ⅱ）原方程可化为令，可得，整理，等价于在有解，利用一元二次方程根的分布求解即可.

试题解析：（Ⅰ） ，∴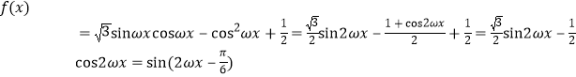

当时，此时单增，不合题意，∴；

∴，∴，在单减，符合题意，故

（Ⅱ），，

方程方程即为：

令，由

，得，于是

原方程化为，整理，等价于在有解

解法一：

（1）当时，方程为得，故；

（2）当时，在上有解在上有解，问题转化为求函数上的值域；设，则，，，

设，在时，单调递减，时，单调递增，∴的取值范围是，

在上有实数解或

解法二：记

（1）当时，，若解得不符合题意，所以；

（2）当，方程在上有解；

①方程在上恰有一解；

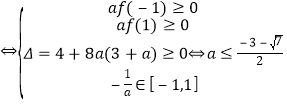②方程在上恰有两解或；

综上所述，的范围是或.