题目内容
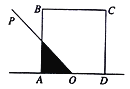
【题目】如图,某生态园将一三角形地块ABC的一角APQ开辟为水果园种植桃树,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.
(1)若围墙AP,AQ总长度为200米,如何围可使得三角形地块APQ的面积最大?
(2)已知AP段围墙高1米,AQ段围墙高1.5米,AP段围墙造价为每平方米150元,AQ段围墙造价为每平方米100元.若围围墙用了30000元,问如何围可使竹篱笆用料最省?
【答案】
(1)解:∵AP+AQ=200,
∴S= ![]() ≤
≤ ![]() =2500
=2500 ![]() .
.
当且仅当x=y=100时取“=”.
∴当x=y=100时,可使得三角形地块APQ的面积最大.
(2)解:设AP=x,AQ=y,则1x150+1.5y100=30000,
化为:x+y=200≥2 ![]() ,可得xy≤10000.
,可得xy≤10000.
∴PQ2=x2+y2﹣2xycos120°=x2+y2+xy=(x+y)2﹣xy=40000﹣xy≥30000.
当且仅当x=y=100时取“=”.
即PQ≥100 ![]() .
.
∴当且仅当x=y=100时,可使PQ取得最小值,即使用竹篱笆用料最省.
【解析】(1)先求出三角形地块APQ的面积,再利用基本不等式可得三角形地块APQ的面积最大;(2)先利用余弦定理可得PQ2,再利用基本不等式可得PQ的最小值.
【考点精析】掌握基本不等式是解答本题的根本,需要知道基本不等式:![]()
![]() ,(当且仅当
,(当且仅当![]() 时取到等号);变形公式:
时取到等号);变形公式:![]()
![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目