题目内容
【题目】已知函数f(x)=sinx,若存在x1 , x2 , ,xm满足0≤x1<x2<xm≤6π,且|f(x1)﹣f(x2)|+|f(x2)﹣f(x3)|+|f(xn﹣1)﹣f(xn)|=12,(m≥2,m∈N*),则m的最小值为 .
【答案】8
【解析】解:∵y=sinx对任意xi,xj(i,j=1,2,3,,m),
都有|f(xi)﹣f(xj)|≤f(x)max﹣f(x)min=2,
要使m取得最小值,尽可能多让xi(i=1,2,3,,m)取得最高点,
考虑0≤x1<x2<<xm≤6π,|f(x1)﹣f(x2)|+|f(x2)﹣f(x3)|++|f(xm﹣1)﹣f(xm)|=12,
按下图取值即可满足条件,
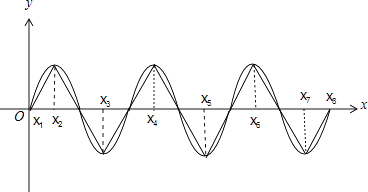
∴m的最小值为8.
所以答案是:8.
【考点精析】利用数列的前n项和对题目进行判断即可得到答案,需要熟知数列{an}的前n项和sn与通项an的关系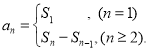 .
.

练习册系列答案
相关题目