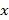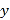题目内容
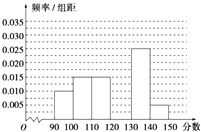
【题目】某县政府为了引导居民合理用水,决定全面实施阶梯水价,阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价:若用水量不超过12吨时,按4元/吨计算水费;若用水量超过12吨且不超过14吨时,超过12吨部分按6.60元/吨计算水费;若用水量超过14吨时,超过14吨部分按7.80元/吨计算水费.为了了解全市居民月用水量的分布情况,通过抽样,获得了100户居民的月用水量(单位:吨),将数据按照![]() ,
,![]() ,…,
,…,![]() 分成8组,制成了如图1所示的频率分布直方图.
分成8组,制成了如图1所示的频率分布直方图.
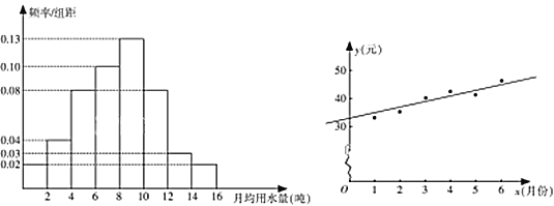
(图1) (图2)
(Ⅰ)通过频率分布直方图,估计该市居民每月的用水量的平均数和中位数(精确到0.01);
(Ⅱ)求用户用水费用![]() (元)关于月用水量
(元)关于月用水量![]() (吨)的函数关系式;
(吨)的函数关系式;
(Ⅲ)如图2是该县居民李某2017年1~6月份的月用水费![]() (元)与月份
(元)与月份![]() 的散点图,其拟合的线性回归方程是
的散点图,其拟合的线性回归方程是![]() .若李某2017年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
.若李某2017年1~7月份水费总支出为294.6元,试估计李某7月份的用水吨数.
【答案】(Ⅰ)平均数为7.96,中位数为8.15;(Ⅱ)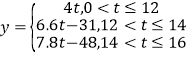 ;(Ⅲ)13吨.
;(Ⅲ)13吨.
【解析】试题分析:
本题考查频率分布直方图的应用及线性回归方程的应用。(Ⅰ)根据用频率分布直方图估计平均数、中位数的方法计算即可。(Ⅱ)结合题意可用分段函数表示出![]() 与
与![]() 的关系。(Ⅲ)先由样本中点过回归直线的结论求得1~6月份月用水费约为
的关系。(Ⅲ)先由样本中点过回归直线的结论求得1~6月份月用水费约为![]() 7月份的水费为
7月份的水费为![]() 元,再根据回归方程求得7月份的用水吨数。
元,再根据回归方程求得7月份的用水吨数。
试题解析:
(Ⅰ)由频率分布直方图可得该市居民每月的用水量的平均数为
![]()
![]() 。
。
设中位数为![]() ,
,
则![]() ,
,
解得![]() 。
。
(Ⅱ)设居民月用水量为![]() 吨,相应的水费为
吨,相应的水费为![]() 元,则由题意得
元,则由题意得
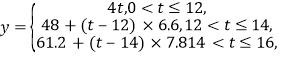
即
(Ⅲ)设李某2017年1~6月份月用水费![]() (元)与月份
(元)与月份![]() 的对应点为
的对应点为![]() ,它们的平均值分别为
,它们的平均值分别为![]() ,
,![]() ,
,
则![]() ,
,
又点![]() 在直线
在直线![]() 上,
上,
所以![]() ,
,
因此![]() ,
,
所以7月份的水费为![]() 元.
元.
由(2)知,当![]() 时,
时,![]() ,
,
所以李某7月份的用水吨数约为13吨.

 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案