题目内容
【题目】已知直线l的参数方程为 ![]() (t为参数),圆C的参数方程为
(t为参数),圆C的参数方程为 ![]() (θ为常数).
(θ为常数).
(1)求直线l和圆C的普通方程;
(2)若直线l与圆C有公共点,求实数a的取值范围.
【答案】
(1)解:直线l的参数方程为 ![]() ,消去t可得2x﹣y﹣2a=0;
,消去t可得2x﹣y﹣2a=0;
圆C的参数方程为 ![]() ,两式平方相加可得x2+y2=16
,两式平方相加可得x2+y2=16
(2)解:圆心C(0,0),半径r=4.
由点到直线的距离公式可得圆心C(0,0)到直线L的距离d= ![]() .
.
∵直线L与圆C有公共点,∴d≤4,即 ![]() ≤4,解得﹣2
≤4,解得﹣2 ![]() ≤a≤2
≤a≤2 ![]()
【解析】(1)消去参数,把直线与圆的参数方程化为普通方程;(2)求出圆心到直线的距离d,再根据直线l与圆C有公共点d≤r即可求出.
【考点精析】解答此题的关键在于理解直线的参数方程的相关知识,掌握经过点![]() ,倾斜角为
,倾斜角为![]() 的直线
的直线![]() 的参数方程可表示为
的参数方程可表示为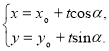 (
(![]() 为参数),以及对圆的参数方程的理解,了解圆
为参数),以及对圆的参数方程的理解,了解圆![]() 的参数方程可表示为
的参数方程可表示为![]() .
.

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
【题目】某中学采取分层抽样的方法从应届高三学生中按照性别抽出20名学生作为样本,其选报文科理科的情况如下表所示.
男 | 女 | |
文科 | 2 | 5 |
理科 | 10 | 3 |
(1)若在该样本中从报考文科的女学生A.B.C.D.E中随机地选出2人召开座谈会,试求2人中有A的概率;
(2)用假设检验的方法分析有多大的把握认为该中学的高三学生选报文理科与性别有关?
参考公式和数据:![]() .
.
P( | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.07 | 2.71 | 3.84 | 5.02 | 6.64 | 7.88 | 10.83 |
