题目内容
求函数f(x)=|x-1|+|2x-1|+|3x-1|+…+|2011x-1|(x∈R)的最小值.
考点:函数的最值及其几何意义
专题:函数的性质及应用
分析:由绝对值的几何意义联想到求距离的最小值,如|x-a|+|x-b|的最小值应该是在数轴上a,b两点之间取得,最小值为|a-b|,
由此把函数f(x)整理为|x-1|+|x-
||+|x-
|+|x-
|+|x-
|+|x-
|+…+|x-
|+|x-
|+|x-
|+…+|x-
|,再用绝对值的意义解题.
由此把函数f(x)整理为|x-1|+|x-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2011 |
| 1 |
| 2011 |
| 1 |
| 2011 |
| 1 |
| 2011 |
解答:
解:由绝对值的几何意义联想到求距离的最小值,如|x-a|+|x-b|的最小值应该是在数轴上a,b两点之间取得,且最小值为|a-b|
所以将函数f(x)的右边整理为|x-1|+|x-
||+|x-
|+|x-
|+|x-
|+|x-
|+…+|x-
|+|x-
|+|x-
|+…+|x-
|,
共有1+2+3+…+2011=1006×2011项,则f(x)可以理解为x 到这1006×2011个点的距离之和
从两端开始向中间靠拢,每两个绝对值和的最小值都是在相应的零点之间取得,而且范围是包含关系,比如|x-1|+|x-
|的
最小值是在x∈[
,1]上取得,再如|x-
|+|x-
|的最小值是在x∈[
,
]上取得,
所以,f(x)的最小值应该在正中间的某个零点或相邻两个零点之间取得,
由
=503×2011 可知取得最小值的范围在第503×2011个零点和第503×2011+1个零点之间(这两个零点也可能相等)
由
<503×2011 算得n≤1421,
所以第503×2011个零点和第503×2011+1个零点均为
则fmin=f(
)=
.
所以将函数f(x)的右边整理为|x-1|+|x-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2011 |
| 1 |
| 2011 |
| 1 |
| 2011 |
| 1 |
| 2011 |
共有1+2+3+…+2011=1006×2011项,则f(x)可以理解为x 到这1006×2011个点的距离之和
从两端开始向中间靠拢,每两个绝对值和的最小值都是在相应的零点之间取得,而且范围是包含关系,比如|x-1|+|x-
| 1 |
| 2011 |
最小值是在x∈[
| 1 |
| 2011 |
| 1 |
| 2 |
| 1 |
| 2011 |
| 1 |
| 2011 |
| 1 |
| 2 |
所以,f(x)的最小值应该在正中间的某个零点或相邻两个零点之间取得,
由
| 1006×2011 |
| 2 |
由
| n×(n+1) |
| 2 |
所以第503×2011个零点和第503×2011+1个零点均为
| 1 |
| 1422 |
则fmin=f(
| 1 |
| 1422 |
| 592043 |
| 711 |
点评:本题主要应用绝对值的意义求解函数的最值,此等类型的题目应合理转化.

练习册系列答案
相关题目
在△ABC中,a,b,c分别为角A,B,C所对的边,若(a+b+c)(sinA+sinB-sinC)=asinB,又sinA=
,则sinB=( )
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
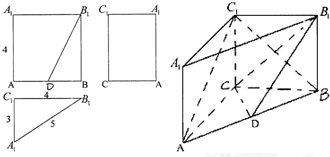
 如图,已知△ABC中,AB=AC=4,∠BAC=90°,D是BC的中点,若向量
如图,已知△ABC中,AB=AC=4,∠BAC=90°,D是BC的中点,若向量